例1
街心花园中间有一个边长为20米的正方形花坛,花坛四周有2米宽的石子路,石子路的面积是多少平方米?
答案:思路分析
根据题意画出示意图如下:
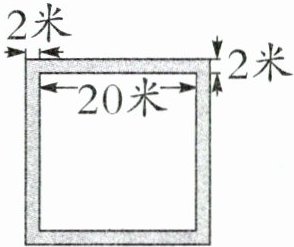
从图中可以看出,石子路的面积=大正方形的面积 - 边长为20米的正方形花坛的面积。大正方形的边长是20 + 2 + 2 = 24(米)。
解答
20 + 2 + 2 = 24(米)
24×24 - 20×20 = 176(平方米)
答:石子路的面积是176平方米。
归纳点拨
考查用直观图表达题意的能力,组合图形的面积可以通过基本图形面积的加或减得出。
1. 实验小学有一个长方形操场,长60米,宽40米。操场扩建时,长增加了15米,宽增加了20米,操场的面积增加了多少平方米?
答案:1. $(60 + 15) × (40 + 20) = 4500$(平方米)
$4500 - 60 × 40 = 2100$(平方米)
【提示】操场扩建后长是 $60 + 15 = 75$(米),宽是 $40 + 20 = 60$(米),用扩建后的面积减原来的面积得出增加的面积。
例2
有一块周长为32分米的正方形玻璃,沿着相邻的两条边各截去2分米,剩下的仍然是一个正方形。截去部分的面积是多少平方分米?
答案:思路分析
根据题意作图如下:
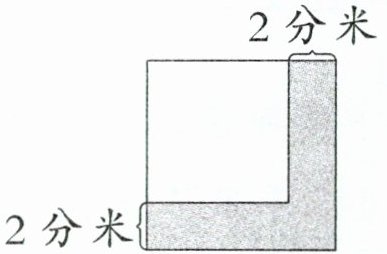
从图中可以看出,截去部分的面积=大正方形的面积 - 空白正方形的面积。
解答
32÷4 = 8(分米)
8 - 2 = 6(分米)
8×8 - 6×6 = 28(平方分米)
答:截去部分的面积是28平方分米。
归纳点拨
解答此类问题的关键是通过画示意图求出大小两个正方形的边长。
2. 如右下图,边长为4厘米的正方形将边长为3厘米的正方形遮住了一部分(涂色部分),两个正方形空白部分的面积差是多少平方厘米?
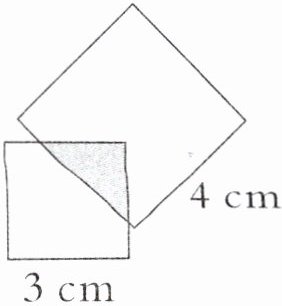
答案:2. $4 × 4 - 3 × 3 = 7$(平方厘米)
【提示】两个正方形的空白部分的面积差相当于两个正方形的面积差,据此求解即可。