例1
甲、乙两地相距645千米,一辆汽车从甲地开往乙地,已经行了5小时,剩下的路程比已经行的多65千米。这辆汽车的平均速度是多少?
答案:思路分析
如下图所示,先根据“甲、乙两地相距645千米”“剩下的路程比已经行的多65千米”这两个条件求出已经行了多少千米,再根据“路程÷时间=速度”求出这辆汽车的平均速度。
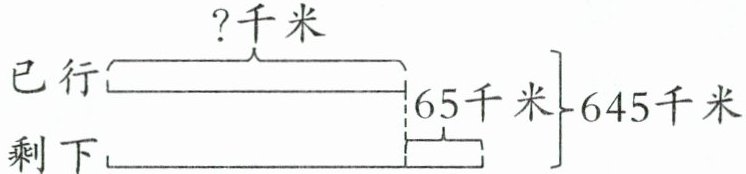
解答
(645 - 65)÷2÷5 = 58(千米/时)
答:这辆汽车的平均速度是58千米/时。
归纳点拨
先用“和差问题”的解题方法求出路程,进而求出速度。
1. 在学校举办的“数学阅读周”活动中,乐乐读的《数学大百科》共295页,他已经读了3天,剩下的页数比已经读的多25页。乐乐平均每天读多少页?
答案:1. $(295 - 25) ÷ 2 ÷ 3 = 45$(页)
【提示】将剩下的页数减去 25 页,就与已经读的页数同样多。将 295 - 25 的差平均分成 2 份,就可以求出已经读的页数,进而求出平均每天读的页数。
例2
甲、乙两个鱼缸里共有金鱼25条,甲鱼缸里新放入6条金鱼,乙鱼缸里取出4条金鱼,这时乙鱼缸比甲鱼缸还多5条金鱼。甲、乙两个鱼缸原来各有多少条金鱼?
答案:思路分析
若甲鱼缸不放入6条金鱼,乙鱼缸不取出4条金鱼,则甲、乙鱼缸原来相差6 + 4 + 5 = 15(条)金鱼,根据“和差问题”的解题方法求解即可。
解答
6 + 4 + 5 = 15(条)
乙鱼缸:(25 + 15)÷2 = 20(条)
甲鱼缸:25 - 20 = 5(条)
答:甲鱼缸原来有5条金鱼,乙鱼缸原来有20条金鱼。
归纳点拨
题中所给条件比较多,还可以通过画图厘清条件,按照“和差问题”的解题方法解答。
2. 姐姐和妹妹共有100元零花钱,如果姐姐给妹妹10元,那么姐姐还比妹妹多6元。姐姐的零花钱原来有多少元?妹妹的零花钱原来有多少元?
答案:2. $10 × 2 + 6 = 26$(元)
姐姐原来:$(100 + 26) ÷ 2 = 63$(元)
妹妹原来:$100 - 63 = 37$(元)
【提示】根据“如果姐姐给妹妹 10 元,那么姐姐还比妹妹多 6 元”可知,原来姐姐比妹妹多 $10 × 2 + 6 = 26$(元)。100 元加 26 元,就是姐姐原来零花钱的 2 倍。