1. (2025·江苏扬州期中·4分)小美同学每天骑电动自行车上学,小美和电动自行车的总质量为120 kg,小美家到学校2 400 m,骑行用时200 s.($g$取10 N/kg)求:
(1) 小美和电动自行车受到的总重力为多少?
(2) 骑行时水平路面对车的支持力是多少?
(3) 小美骑自行车的速度为多少?
(4) 若自行车车受到的阻力为车总重的$\frac{1}{10}$,则骑行时自行车受到的阻力为多少?
答案:1.(1)1 200 N (2)1 200 N (3)12 m/s (4)120 N 解析:(1)小美和电动自行车受到的总重力$G=mg=120 \mathrm{ kg} × 10 \mathrm{ N/kg}=1 200 \mathrm{ N}$.(2)根据二力平衡,骑行时水平路面对车的支持力$F_{\mathrm{支}}=G=1 200 \mathrm{ N}$.(3)小美骑自行车的速度$v = \frac{s}{t} = \frac{2 400 \mathrm{ m}}{200 \mathrm{ s}} = 12 \mathrm{ m/s}$.(4)骑行时自行车受到的阻力$f = \frac{1}{10}G = \frac{1}{10} × 1 200 \mathrm{ N} = 120 \mathrm{ N}$.
解析:
(1)已知总质量$m = 120\ \mathrm{kg}$,$g = 10\ \mathrm{N/kg}$,根据重力公式$G=mg$,可得总重力$G=120\ \mathrm{kg}×10\ \mathrm{N/kg}=1200\ \mathrm{N}$。
(2)因为在水平路面骑行时,车在竖直方向静止,支持力与重力平衡,所以支持力$F_{\mathrm{支}}=G = 1200\ \mathrm{N}$。
(3)已知路程$s = 2400\ \mathrm{m}$,时间$t=200\ \mathrm{s}$,根据速度公式$v=\frac{s}{t}$,可得速度$v=\frac{2400\ \mathrm{m}}{200\ \mathrm{s}}=12\ \mathrm{m/s}$。
(4)由题意,阻力$f=\frac{1}{10}G$,则$f=\frac{1}{10}×1200\ \mathrm{N}=120\ \mathrm{N}$。
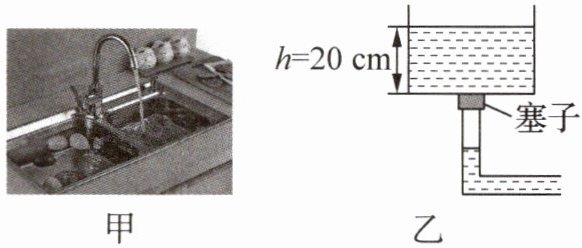
2. (2025·安徽淮北期中·6分)小溪在厨房的水槽内洗碗时(如图甲所示),发现水槽内的水越深,水槽底部的塞子越难拔起.水池近似于长方体盛水器皿,在池底有一横截面积为50 cm²的塞子(如图乙所示),此时蓄水深度约为20 cm.请用所学的知识回答以下问题.($g$取10 N/kg,$\rho_{水}$=1.0×10³ kg/m³)
(1) 求池底处所受液体压强.
(2) 求池水对塞子的压力.
(3) 若塞子重1 N,则竖直向上至少要用多大的拉力$F_{拉}$才能将塞子取走?
答案:2.(1)$2 × 10^{3} \mathrm{ Pa}$ (2)10 N (3)11 N 解析:(1)池底所受液体的压强$p = \rho_{\mathrm{水}} gh = 1.0 × 10^{3} \mathrm{ kg/m}^{3} × 10 \mathrm{ N/kg} × 20 × 10^{-2} \mathrm{ m} = 2 × 10^{3} \mathrm{ Pa}$.(2)由$p = \frac{F}{S}$可知,池水对塞子的压力$F = pS = 2 × 10^{3} \mathrm{ Pa} × 50 × 10^{-4} \mathrm{ m}^{2} = 10 \mathrm{ N}$.(3)对塞子进行受力分析,刚好能将塞子取走时塞子受到竖直向下的重力、竖直向下的压力和竖直向上的拉力,三力平衡,即$F_{\mathrm{拉}} = G + F$,则竖直向上的拉力$F_{\mathrm{拉}} = G + F = 1 \mathrm{ N} + 10 \mathrm{ N} = 11 \mathrm{ N}$.所以要至少要用11 N的拉力才能将塞子取走.
解析:
(1)解:池底所受液体的压强:$p = \rho_{\mathrm{水}}gh = 1.0×10^{3}\ \mathrm{kg/m}^{3}×10\ \mathrm{N/kg}×20×10^{-2}\ \mathrm{m} = 2×10^{3}\ \mathrm{Pa}$
(2)解:塞子的横截面积:$S = 50\ \mathrm{cm}^{2} = 50×10^{-4}\ \mathrm{m}^{2}$,由$p=\frac{F}{S}$得,池水对塞子的压力:$F = pS = 2×10^{3}\ \mathrm{Pa}×50×10^{-4}\ \mathrm{m}^{2} = 10\ \mathrm{N}$
(3)解:竖直向上的拉力:$F_{\mathrm{拉}} = G + F = 1\ \mathrm{N} + 10\ \mathrm{N} = 11\ \mathrm{N}$
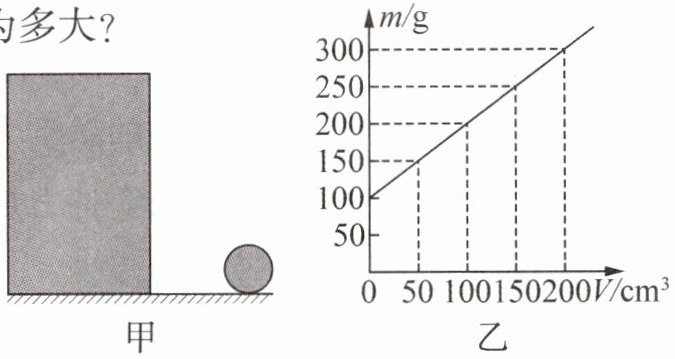
3. (8分)如图甲所示,容积为600 cm³的圆柱形容器和一个体积为80 cm³的金属铝球置于水平桌面上,容器内盛某种液体时,容器和液体的总质量与液体体积的关系如图乙所示.($\rho_{铝}$=2.7×10³ kg/m³)求:
(1) 该液体的密度是多少?
(2) 容器内盛满这种液体后,液体和容器的总质量是多少?
(3) 容器内盛满这种液体后,再将小球轻轻地放入容器中,小球沉入容器底,待液体溢尽,擦干容器壁,测得容器、水和小球的总质量为809 g,小球的质量为多少?
(4) 该小球是实心还是空心?如果是空心,则空心体积为多大?
答案:3.(1)$1 \mathrm{ g/cm}^{3}$ (2)700 g (3)189 g (4)该小球是空心的,空心体积为$10 \mathrm{ cm}^{3}$ 解析:(1)由图乙可知,液体体积为0时的总质量为100 g,则容器的质量$m_{\mathrm{容器}} = 100 \mathrm{ g}$,液体体积为$V_{\mathrm{液}} = 200 \mathrm{ cm}^{3}$时,容器和液体的总质量$m_{\mathrm{总}} = 300 \mathrm{ g}$,则液体的质量$m_{\mathrm{液}} = m_{\mathrm{总}} - m_{\mathrm{容器}} = 300 \mathrm{ g} - 100 \mathrm{ g} = 200 \mathrm{ g}$,液体的密度$\rho_{\mathrm{液}} = \frac{m_{\mathrm{液}}}{V_{\mathrm{液}}} = \frac{200 \mathrm{ g}}{200 \mathrm{ cm}^{3}} = 1 \mathrm{ g/cm}^{3}$.(2)容器内盛满这种液体时,液体的体积$V_{\mathrm{液}}' = V_{\mathrm{容}} = 600 \mathrm{ cm}^{3}$,由$\rho = \frac{m}{V}$可得,液体的质量$m_{\mathrm{液}}' = \rho_{\mathrm{液}} V_{\mathrm{液}}' = 1 \mathrm{ g/cm}^{3} × 600 \mathrm{ cm}^{3} = 600 \mathrm{ g}$,容器和液体的总质量$m_{\mathrm{总}}' = m_{\mathrm{容器}} + m_{\mathrm{液}}' = 100 \mathrm{ g} + 600 \mathrm{ g} = 700 \mathrm{ g}$.(3)容器内盛满这种液体后,再将小球轻轻地放入容器中,小球沉入容器底,则小球排开液体的体积$V_{\mathrm{溢}} = V_{\mathrm{球}} = 80 \mathrm{ cm}^{3}$,溢出液体的质量$m_{\mathrm{溢}} = \rho_{\mathrm{液}} V_{\mathrm{溢}} = 1 \mathrm{ g/cm}^{3} × 80 \mathrm{ cm}^{3} = 80 \mathrm{ g}$,待液体溢尽,擦干容器壁,测得容器、水和小球的总质量为809 g,因为$m_{\mathrm{剩}} = m_{\mathrm{容器}} + m_{\mathrm{液}}' + m_{\mathrm{球}} - m_{\mathrm{溢}}$,则小球的质量$m_{\mathrm{球}} = m_{\mathrm{剩}} + m_{\mathrm{溢}} - m_{\mathrm{液}}' - m_{\mathrm{容器}} = 809 \mathrm{ g} + 80 \mathrm{ g} - 600 \mathrm{ g} - 100 \mathrm{ g} = 189 \mathrm{ g}$.(4)小球中铝的体积$V_{\mathrm{铝}} = \frac{m_{\mathrm{球}}}{\rho_{\mathrm{铝}}} = \frac{189 \mathrm{ g}}{2.7 \mathrm{ g/cm}^{3}} = 70 \mathrm{ cm}^{3}$,铝的体积小于球的体积,说明球是空心的,球空心部分的体积$V = V_{\mathrm{球}} - V_{\mathrm{铝}} = 80 \mathrm{ cm}^{3} - 70 \mathrm{ cm}^{3} = 10 \mathrm{ cm}^{3}$.
解析:
(1)由图乙可知,当液体体积$V_{\mathrm{液}}=0$时,总质量$m_{\mathrm{总}}=100\ \mathrm{g}$,则容器质量$m_{\mathrm{容器}}=100\ \mathrm{g}$。当$V_{\mathrm{液}}=200\ \mathrm{cm}^3$时,$m_{\mathrm{总}}=300\ \mathrm{g}$,液体质量$m_{\mathrm{液}}=300\ \mathrm{g}-100\ \mathrm{g}=200\ \mathrm{g}$,液体密度$\rho_{\mathrm{液}}=\frac{m_{\mathrm{液}}}{V_{\mathrm{液}}}=\frac{200\ \mathrm{g}}{200\ \mathrm{cm}^3}=1\ \mathrm{g/cm}^3$。
(2)容器容积$V_{\mathrm{容}}=600\ \mathrm{cm}^3$,盛满液体时$V_{\mathrm{液}}'=600\ \mathrm{cm}^3$,液体质量$m_{\mathrm{液}}'=\rho_{\mathrm{液}}V_{\mathrm{液}}'=1\ \mathrm{g/cm}^3×600\ \mathrm{cm}^3=600\ \mathrm{g}$,总质量$m_{\mathrm{总}}'=m_{\mathrm{容器}}+m_{\mathrm{液}}'=100\ \mathrm{g}+600\ \mathrm{g}=700\ \mathrm{g}$。
(3)小球体积$V_{\mathrm{球}}=80\ \mathrm{cm}^3$,沉入容器后排开液体体积$V_{\mathrm{溢}}=V_{\mathrm{球}}=80\ \mathrm{cm}^3$,溢出液体质量$m_{\mathrm{溢}}=\rho_{\mathrm{液}}V_{\mathrm{溢}}=1\ \mathrm{g/cm}^3×80\ \mathrm{cm}^3=80\ \mathrm{g}$。由$m_{\mathrm{剩}}=m_{\mathrm{容器}}+m_{\mathrm{液}}'+m_{\mathrm{球}}-m_{\mathrm{溢}}$,得$m_{\mathrm{球}}=m_{\mathrm{剩}}+m_{\mathrm{溢}}-m_{\mathrm{容器}}-m_{\mathrm{液}}'=809\ \mathrm{g}+80\ \mathrm{g}-100\ \mathrm{g}-600\ \mathrm{g}=189\ \mathrm{g}$。
(4)$\rho_{\mathrm{铝}}=2.7\ \mathrm{g/cm}^3$,铝的体积$V_{\mathrm{铝}}=\frac{m_{\mathrm{球}}}{\rho_{\mathrm{铝}}}=\frac{189\ \mathrm{g}}{2.7\ \mathrm{g/cm}^3}=70\ \mathrm{cm}^3$。因为$V_{\mathrm{铝}}=70\ \mathrm{cm}^3< V_{\mathrm{球}}=80\ \mathrm{cm}^3$,所以小球是空心的,空心体积$V_{\mathrm{空}}=V_{\mathrm{球}}-V_{\mathrm{铝}}=80\ \mathrm{cm}^3-70\ \mathrm{cm}^3=10\ \mathrm{cm}^3$。
(1)$1\ \mathrm{g/cm}^3$;(2)$700\ \mathrm{g}$;(3)$189\ \mathrm{g}$;(4)空心,$10\ \mathrm{cm}^3$。