11. 新趋势 项
目式探究(2025·广西南宁三模·7 分)研究表明:多种疾病风险的增加与高糖摄入有关,高糖摄入的重灾区就是含糖饮料.饮料的含糖量是一个重要的指标,项目小组想研究某种碳酸饮料的含糖量,经查阅文献得知,饮料含糖量$Y$与其密度$\rho$存在如下近似关系:$Y = 2.76×(\frac{\rho}{\rho_{水}} - 1)×100\%$,其中$\rho_{水}=1.0\ \mathrm{g}/\mathrm{cm}^{3}$.
【任务驱动】测量某种碳酸饮料的密度.
【方案实施】用天平、量筒等测量该饮料的密度.
① 将天平放在
水平
桌面上,调节天平横梁平衡时,先把
游码
移到标尺左端零刻度线处,若指针静止时指在分度盘中央刻度线的右侧,则应向
左
(选填“左”或“右”)调节平衡螺母,使横梁平衡.
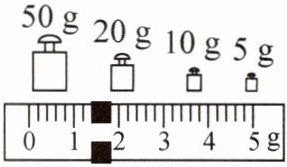
② 在烧杯中倒入适量饮料,置于天平左盘,测出其总质量如图甲所示,为
86.4
$g$.
③ 再将烧杯中的饮料倒入量筒中测出其体积,但饮料太多,无法全部倒入量筒中.经小组讨论,只需增加一个步骤用天平测出
烧杯中剩余饮料和烧杯
的质量,即可求出饮料的密度.
【方案迭代】项目小组成员采用另一种方法测量该饮料的密度:
① 将一电子秤放在水平台面上,启动“开关”后,放上空烧杯,并按下“去皮”键将示数清零;
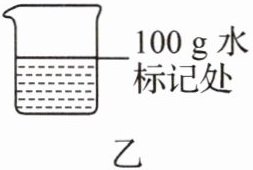
② 向烧杯中倒水,直至示数达到$100\ \mathrm{g}$.在液面处用笔做好标记,如图乙所示;
③ 将杯中的水倒掉后,擦干烧杯放回电子秤上,按下“去皮”键,再倒入饮料至标记处,此时电子秤的示数为$108\ \mathrm{g}$.则该饮料的密度为
1.08
$\mathrm{g}/\mathrm{cm}^{3}$.
【项目成果】以第二种方法测得的密度值为准,该碳酸饮料的含糖量为
22
$\%$(保留整数).
答案:11.【方案实施】①水平 游码 左 ②86.4 ③烧杯中剩余饮料和烧杯 【方案迭代】③1.08 【项目成果】22 解析:【方案实施】①使用天平时,要将天平放在水平桌面上.调节天平横梁平衡时,先把游码移到标尺左端零刻度线处,即游码归零,若指针静止时指在分度盘中央刻度线的右侧,说明右侧重,应向左调节平衡螺母,使横梁平衡. ②在烧杯中倒入适量饮料,置于天平左盘,测出其总质量如图甲所示,标尺的分度值为0.2 g,游码在标尺上的读数是1.4 g,则总质量$m = 50\ g + 20\ g + 10\ g + 5\ g + 1.4\ g = 86.4\ g$.
③要求出饮料的密度,只需要知道量筒中饮料的质量和体积,则需要增加的步骤:用天平测出烧杯中剩余饮料和烧杯的质量,该质量与②中总质量的差值即为量筒中饮料的质量.【方案迭代】③由操作过程可知,水和饮料的体积相等,由密度公式可知$\frac{m_{水}}{\rho_{水}} = \frac{m_{饮料}}{\rho_{饮料}}$,该饮料的密度$\rho_{饮料} = \frac{m_{饮料}}{m_{水}}\rho_{水} = \frac{108\ g}{100\ g} × 1.0\ g/cm^3 = 1.08\ g/cm^3$.【项目成果】饮料含糖量为$Y = 2.76 × (\frac{\rho_{饮料}}{\rho_{水}} - 1) × 100\% = 2.76 × (\frac{1.08\ g/cm^3}{1.0\ g/cm^3} - 1) × 100\% = 22.08\% \approx 22\%$.
12.(8 分)一个底面积为$100\ \mathrm{cm}^{2}$的薄壁柱形容器放在水平电子秤上,向容器中缓慢注入液体,停止注入液体时,容器中液体的深度为$4\ \mathrm{cm}$;将均匀实心柱体缓慢放入液体中,放手后,柱体静止时如图甲所示;整个过程,电子秤的示数与容器内液体深度的关系如图乙所示.求:
(1)容器的质量为
50
$g$.
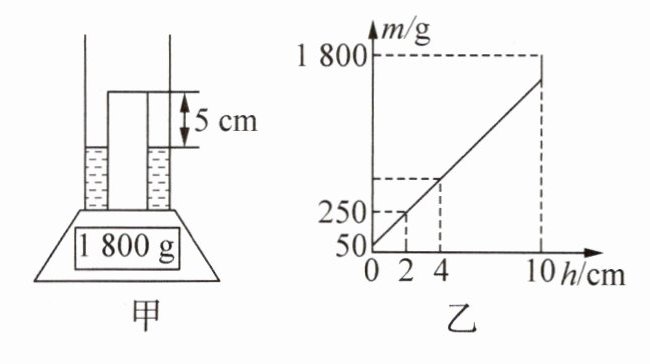
(2)液体的密度.
(3)停止注入液体时,容器的总质量.
(4)实心柱体的密度.
答案:12. (1)50 g (2)$1\ g/cm^3$ (3)450 g (4)$1.5\ g/cm^3$
解析:(1)由图乙可知,当液体深度为零时,电子秤的示数为50 g,所以容器的质量$m_{容} = 50\ g$.(2)当液体的深度为2 cm时,液体和容器的总质量$m_{总} = 250\ g$,此时液体的质量$m_{液} = m_{总} - m_{容器} = 250\ g - 50\ g = 200\ g$,液体的体积$V_{液} = S_{容器}h_1 = 100\ cm^2 × 2\ cm = 200\ cm^3$,液体的密度$\rho_{液} = \frac{m_{液}}{V_{液}} = \frac{200\ g}{200\ cm^3} = 1\ g/cm^3$.(3)当$h_2 = 4\ cm$时,停止注入液体,此时液体的体积$V_{液}' = S_{容器}h_2 = 100\ cm^2 × 4\ cm = 400\ cm^3$,则液体的质量$m_{液}' = \rho_{液}V_{液}' = 1\ g/cm^3 × 400\ cm^3 = 400\ g$,故容器和液体的总质量$m_{总}' = m_{液}' + m_{容器} = 400\ g + 50\ g = 450\ g$.(4)由图甲可得,放入柱体后,柱体未浸入液体的高度为5 cm,电子秤示数为1800 g,柱体的质量为$m_{柱} = m_{总}'' - m_{总}' = 1800\ g - 450\ g = 1350\ g$,设柱体的底面积为$S_{柱}$,由图乙可知液体的最大深度$h_{最大} = 10\ cm$,又$V_{液}'$不变,则有$(S_{容器} - S_{柱})h_{最大} = V_{液}'$,柱体的底面积$S_{柱} = S_{容器} - \frac{V_{液}'}{h_{最大}} = 100\ cm^2 - \frac{400\ cm^3}{10\ cm} = 60\ cm^2$,柱体的高度$h_{柱} = h_{最大} + h = 10\ cm + 5\ cm = 15\ cm$,所以柱体的体积$V_{柱} = S_{柱}h_{柱} = 60\ cm^2 × 15\ cm = 900\ cm^3$,柱体的密度$\rho_{柱} = \frac{m_{柱}}{V_{柱}} = \frac{1350\ g}{900\ cm^3} = 1.5\ g/cm^3$.