10. 如图,在平面直角坐标系中,$\odot M$经过$O(0,0)$,$A(0,4)$,$B(3,0)$三点,$P$为$\odot M$上一点,且在第一象限,则$\sin P$的值为
$\frac{4}{5}$
.

]
答案:10.$\frac{4}{5}$
解析:
解:连接 $AB$,
$\because A(0,4)$,$B(3,0)$,$O(0,0)$,
$\therefore OA=4$,$OB=3$,$\angle AOB=90°$,
$\therefore AB=\sqrt{OA^2 + OB^2}=\sqrt{4^2 + 3^2}=5$,
$\because \angle P$ 与 $\angle O$ 所对的弧均为 $\overset{\frown}{AB}$,
$\therefore \angle P = \angle O = 90°$(此处错误,应为$\angle P = \angle OAB$或$\angle P = \angle OBA$,正确推导如下:)
$\because \angle ABP$ 与 $\angle AOP$ 所对的弧均为 $\overset{\frown}{AP}$,
$\therefore \angle ABP = \angle AOP$,同理$\angle BAP = \angle BOP$,
$\therefore \triangle ABP ∼ \triangle AOB$(相似条件不充分,正确利用同弧所对圆周角相等:$\angle P = \angle OAB$,因为$\angle P$和$\angle OAB$都对$\overset{\frown}{OB}$)
$\because \angle P$ 和 $\angle OAB$ 都对 $\overset{\frown}{OB}$,
$\therefore \angle P = \angle OAB$,
在 $Rt\triangle AOB$ 中,$\sin \angle OAB = \frac{OB}{AB} = \frac{3}{5}$(错误,$\sin \angle OAB = \frac{OB}{AB} = \frac{3}{5}$,$\sin \angle OBA = \frac{OA}{AB} = \frac{4}{5}$,$\angle P$ 应等于$\angle OBA$)
$\because \angle P$ 和 $\angle OBA$ 都对 $\overset{\frown}{OA}$,
$\therefore \angle P = \angle OBA$,
$\sin \angle OBA = \frac{OA}{AB} = \frac{4}{5}$,
$\therefore \sin P = \frac{4}{5}$。
$\frac{4}{5}$
11. 亮点原创·新趋势
传统文化《九章算术》是我国古代数学成就的杰出代表,其中《方田》章给出计算弧田面积的经验公式(求出的结果为近似值):弧田面积$ = \dfrac{1}{2}$(弦$×$矢$ + $矢$^{2}$),其中弧田由圆弧和其所对的弦围成,公式中“弦”指圆弧所对弦长,“矢”等于半径与圆心到弦的距离之差.在如图所示的弧田中,$O$是圆弧所在圆的圆心,$AB$是“弦”.若“矢”为$3$,$\cos \angle OAB = \dfrac{24}{25}$,则根据经验公式,该弧田的面积为
$\frac{33}{2}$
.
]

答案:11.$\frac{33}{2}$
解析:
解:设圆的半径为$r$,圆心$O$到弦$AB$的距离为$d$,则矢$=r - d = 3$,即$d = r - 3$。
过$O$作$OC ⊥ AB$于$C$,则$AC = \frac{1}{2}AB$,$OC = d = r - 3$。
在$Rt\triangle AOC$中,$\cos \angle OAB = \frac{AC}{OA} = \frac{AC}{r} = \frac{24}{25}$,所以$AC = \frac{24}{25}r$。
由勾股定理得:$AC^2 + OC^2 = OA^2$,即$(\frac{24}{25}r)^2 + (r - 3)^2 = r^2$。
解得$r = 25$($r = \frac{25}{16}$舍去),则$d = 25 - 3 = 22$,$AC = \frac{24}{25} × 25 = 24$,弦$AB = 2AC = 48$。
弧田面积$= \frac{1}{2}(\mathrm{弦} × \mathrm{矢} + \mathrm{矢}^2) = \frac{1}{2}(48 × 3 + 3^2) = \frac{1}{2}(144 + 9) = \frac{153}{2}$。
1
12. 在$\triangle ABC$中,若$AB = 7$,$AC = 8$,$BC = 5$,则$\sin C =$
$\frac{\sqrt{3}}{2}$
.
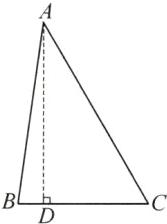
答案:12.$\frac{\sqrt{3}}{2}$ 解析:如图,过点A作AD⊥BC于点D,则∠ADB = ∠ADC = 90°,所以$AD^2 + BD^2 = AB^2$,$AD^2 + CD^2 = AC^2$,所以$AB^2 - BD^2 = AC^2 - CD^2$.设BD = x.因为BC = 5,所以CD = BC - BD = 5 - x.因为AB = 7,AC = 8,所以$7^2 - x^2 = 8^2 - (5 - x)^2$,解得x = 1,所以CD = 4,所以$AD = \sqrt{AC^2 - CD^2} = 4\sqrt{3}$,所以$\sin C = \frac{AD}{AC} = \frac{\sqrt{3}}{2}$.
13. (2024·江苏苏州)如图,在$\triangle ABC$中,$AB = 4\sqrt{2}$,$D$为$AB$的中点,$\angle BAC = \angle BCD$,$\cos \angle ADC = \dfrac{\sqrt{2}}{4}$,$\odot O$是$\triangle ACD$的外接圆.
(1) 求$BC$的长;
(2) 求$\odot O$的半径.

]
答案:13.(1)因为$AB = 4\sqrt{2}$,D为AB的中点,所以$AD = BD = \frac{1}{2}AB = 2\sqrt{2}$.因为∠BAC = ∠BCD,∠ABC = ∠CBD,所以△ABC∽△CBD,所以$\frac{AB}{BC} = \frac{BC}{BD}$,所以$BC^2 = AB · BD = 16$,所以BC = 4.
(2)连接OC,过点A作AE⊥CD于点E,则∠AEC = ∠AED = 90°.因为$\cos∠ADC = \frac{\sqrt{2}}{4}$,所以$\frac{DE}{AD} = \frac{\sqrt{2}}{4}$.因为$AD = 2\sqrt{2}$,所以DE = 1,所以$AE = \sqrt{AD^2 - DE^2} = \sqrt{7}$.因为△ABC∽△CBD,所以$\frac{AC}{CD} = \frac{AB}{BC}$.因为$AB = 4\sqrt{2}$,BC = 4,所以$\frac{AC}{CD} = \sqrt{2}$.设CD = x,则$AC = \sqrt{2}x$,CE = CD - DE = x - 1.因为$AE^2 + CE^2 = AC^2$,所以$(\sqrt{7})^2 + (x - 1)^2 = (\sqrt{2}x)^2$,解得$x_1 = 2$,$x_2 = -4$(不合题意,舍去),所以CE = 1,AC = $2\sqrt{2}$,所以AC = AD,所以AE垂直平分CD,所以点O在线段AE上.设⊙O的半径为r,则OA = OC = r,$OE = AE - OA = \sqrt{7} - r$.因为∠OEC = 90°,所以$OE^2 + CE^2 = OC^2$,所以$(\sqrt{7} - r)^2 + 1^2 = r^2$,解得$r = \frac{4\sqrt{7}}{7}$.故⊙O的半径为$\frac{4\sqrt{7}}{7}$.
14. (2025·江苏徐州模拟)如图,在等腰直角三角形$ABC$中,$\angle C = 90^{\circ}$,$D$为$BC$的中点,将$\triangle ABC$折叠,使点$A$与点$D$重合,$EF$为折痕,则$\sin \angle BED$的值是(
B
)

A.$\dfrac{\sqrt{5}}{3}$
B.$\dfrac{3}{5}$
C.$\dfrac{2\sqrt{2}}{3}$
D.$\dfrac{2}{3}$
答案:14.B 解析:因为△ABC是等腰直角三角形,∠C = 90°,所以CA = CB,∠A = ∠B = 45°.由折叠的性质,得DF = AF,∠EDF = ∠A = 45°.因为∠CDE = ∠BED + ∠B = ∠CDF + ∠EDF,所以∠BED = ∠CDF.设CD = 1,CF = x.因为D为BC的中点,所以CA = CB = 2CD = 2,所以DF = AF = CA - CF = 2 - x.因为$CF^2 + CD^2 = DF^2$,所以$x^2 + 1^2 = (2 - x)^2$,解得$x = \frac{3}{4}$,所以$CF = \frac{3}{4}$,$DF = \frac{5}{4}$,所以$\sin∠BED = \sin∠CDF = \frac{CF}{DF} = \frac{3}{5}$.
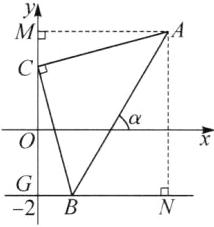
15. 如图,在平面直角坐标系中,$O$是原点,点$A(4,3)$,$B$为直线$y = - 2$上的一动点,点$C(0,n)$,$- 2 < n < 3$,$AC ⊥ BC$,连接$AB$.若直线$AB$与$x$轴正半轴所夹的锐角为$\alpha$,则当$\sin \alpha$的值最大时,$n$的值为
$\frac{1}{2}$
.
]

答案:15.$\frac{1}{2}$ 解析:如图,过点A作AM⊥y轴,AN⊥直线y = -2,垂足分别为M,N,则∠AMC = ∠ANB = 90°.因为BN//x轴,所以∠ABN = α.因为sinα的值最大时,tanα的值也最大,且$\tanα = \tan∠ABN = \frac{AN}{BN}$,AN的长为定值,所以当BN的长最小时,sinα的值最大.设直线y = -2与y轴交于点G,则G(0, -2),所以OG = 2.因为A(4,3),所以NG = AM = 4,OM = 3,所以AN = MG = OM + OG = 5,BN = NG - BG = 4 - BG,所以当BG的长最大时,BN的长最小.因为AC⊥BC,所以∠ACB = 90°,所以∠ACM + ∠BCG = 180° - ∠ACB = 90°.因为∠ACM + ∠CAM = 90°,所以∠BCG = ∠CAM.又∠CGB = ∠AMC,所以△BCG∽△CAM,所以$\frac{BG}{CM} = \frac{CG}{AM}$.设BG = m.因为C(0,n),所以CM = 3 - n,CG = n + 2,所以$\frac{m}{3 - n} = \frac{n + 2}{4}$,所以$m = -\frac{1}{4}n^2 + \frac{1}{4}n + \frac{3}{2} = -\frac{1}{4}(n - \frac{1}{2})^2 + \frac{25}{16}$.因为$-\frac{1}{4} < 0$,-2 < n < 3,所以当$n = \frac{1}{2}$时,m取最大值,即sinα的值最大.
16. 新素养
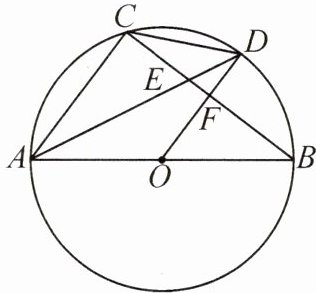
推理能力 如图,$AB$为$\odot O$的直径,$C$为$\odot O$上一点,$D$为$\overset{\frown}{BC}$的中点,$BC$与$AD$,$OD$分别交于点$E$,$F$.
(1) 求证:$DO // AC$;
(2) 求证:$DE · DA = DC^{2}$;
(3) 若$\tan \angle CAD = \dfrac{1}{2}$,求$\sin \angle CDA$的值.
]
答案:16.(1)因为D为BC的中点,所以$\overset{\frown}{CD} = \overset{\frown}{DB}$,所以∠CAD = ∠BAD,所以∠BAC = 2∠BAD.因为∠BOD = 2∠BAD,所以∠BAC = ∠BOD,所以DO//AC.
(2)因为$\overset{\frown}{CD} = \overset{\frown}{DB}$,所以∠CAD = ∠ECD.又∠ADC = ∠CDE,所以△ACD∽△CED,所以$\frac{DA}{DC} = \frac{DC}{DE}$,所以$DE · DA = DC^2$.
(3)连接BD.因为AB为⊙O的直径,所以∠ACB = 90°.因为DO//AC,所以∠OFB = ∠ACB = 90°,所以∠BFD = 180° - ∠OFB = 90°.因为∠CAD = ∠CBD,所以$\tan∠CBD = \tan∠CAD = \frac{1}{2}$,所以$\frac{DF}{BF} = \frac{1}{2}$.设DF = k,则BF = 2k.设OB = OD = r,则OF = OD - DF = r - k.因为$OF^2 + BF^2 = OB^2$,所以$(r - k)^2 + (2k)^2 = r^2$.整理,得$r = \frac{5}{2}k$,所以$OF = \frac{3}{2}k$,所以$\sin∠CBA = \frac{OF}{OB} = \frac{3}{5}$.因为∠CDA = ∠CBA,所以$\sin∠CDA = \sin∠CBA = \frac{3}{5}$.