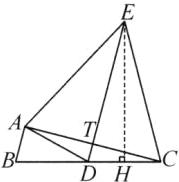
1. 如图,在$\triangle ABC$中,$CA = CB = 4$,$\cos C = \dfrac{1}{4}$,则$\sin B$的值为(
D
)
A.$\dfrac{\sqrt{10}}{2}$
B.$\dfrac{\sqrt{15}}{3}$
C.$\dfrac{\sqrt{6}}{4}$
D.$\dfrac{\sqrt{10}}{4}$
答案:1.D
解析:
过点$A$作$AD ⊥ BC$于点$D$。
在$\triangle ADC$中,$CA = 4$,$\cos C=\dfrac{1}{4}$,则$CD=CA·\cos C = 4×\dfrac{1}{4}=1$,$AD=\sqrt{CA^{2}-CD^{2}}=\sqrt{4^{2}-1^{2}}=\sqrt{15}$。
因为$CB = 4$,所以$BD=CB - CD=4 - 1=3$。
在$\triangle ABD$中,$AD=\sqrt{15}$,$BD = 3$,则$AB=\sqrt{AD^{2}+BD^{2}}=\sqrt{(\sqrt{15})^{2}+3^{2}}=\sqrt{15 + 9}=\sqrt{24}=2\sqrt{6}$。
在$\triangle ABC$中,由正弦定理$\dfrac{AC}{\sin B}=\dfrac{AB}{\sin C}$。
$\sin C=\sqrt{1-\cos^{2}C}=\sqrt{1 - (\dfrac{1}{4})^{2}}=\sqrt{\dfrac{15}{16}}=\dfrac{\sqrt{15}}{4}$。
所以$\sin B=\dfrac{AC·\sin C}{AB}=\dfrac{4×\dfrac{\sqrt{15}}{4}}{2\sqrt{6}}=\dfrac{\sqrt{15}}{2\sqrt{6}}=\dfrac{\sqrt{15}×\sqrt{6}}{2×6}=\dfrac{\sqrt{90}}{12}=\dfrac{3\sqrt{10}}{12}=\dfrac{\sqrt{10}}{4}$。
D
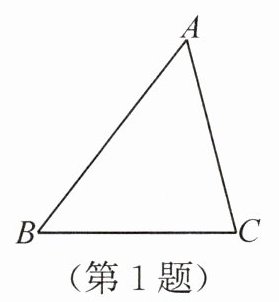
2. 如图,在菱形$ABCD$中,$DE ⊥ AB$,垂足为$E$.若$\cos A = \dfrac{3}{5}$,则$\sin \angle DBE$的值是(
D
)
A.$\dfrac{1}{2}$
B.$2$
C.$\dfrac{\sqrt{5}}{5}$
D.$\dfrac{2\sqrt{5}}{5}$
答案:2.D 解析:因为DE⊥AB,所以∠DEA=∠DEB=90°,所以$\cos A = \frac{AE}{AD} = \frac{3}{5}$.设AE = 3x,则AD = 5x,所以$DE = \sqrt{AD^2 - AE^2} = 4x$.因为四边形ABCD为菱形,所以AB = AD = 5x,所以BE = AB - AE = 2x,所以$BD = \sqrt{DE^2 + BE^2} = 2\sqrt{5}x$,所以$\sin∠DBE = \frac{DE}{BD} = \frac{2\sqrt{5}}{5}$.
3. (教材$P104$习题$5$变式)若$\alpha$是锐角,且$\sin \alpha = \dfrac{3}{5}$,则$\cos \alpha =$
$\frac{4}{5}$
.
答案:3.$\frac{4}{5}$
4. 新素养 几何直观 如图,$\angle AOB$是放置在正方形网格中的一个角,则$\sin \angle AOB =$
$\frac{\sqrt{2}}{2}$
.
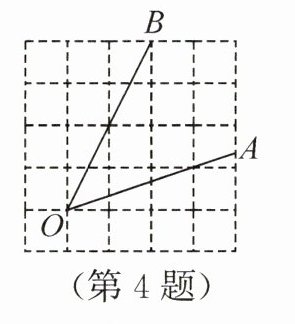
答案:4.$\frac{\sqrt{2}}{2}$
5. 如图,$\odot O$的直径$AB$经过弦$CD$的中点$H$.若$\cos \angle CDB = \dfrac{4}{5}$,$BD = 5$,则$\odot O$的半径为
$\frac{25}{6}$
.
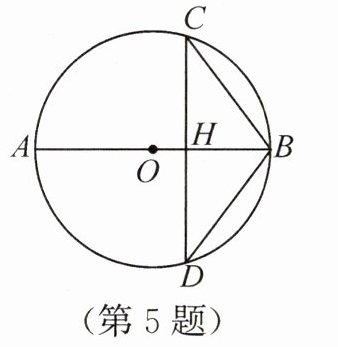
答案:5.$\frac{25}{6}$ 解析:连接OD.因为⊙O的直径AB经过弦CD的中点H,所以AB⊥CD,所以∠OHD=∠BHD=90°,所以$\cos∠CDB = \frac{DH}{BD} = \frac{4}{5}$.因为BD = 5,所以DH = 4,所以$BH = \sqrt{BD^2 - DH^2} = 3$.设OB = OD = r,则OH = OB - BH = r - 3.因为$OH^2 + DH^2 = OD^2$,所以$(r - 3)^2 + 4^2 = r^2$,解得$r = \frac{25}{6}$.故⊙O的半径为$\frac{25}{6}$.
解析:
解:连接$OD$。
因为$\odot O$的直径$AB$经过弦$CD$的中点$H$,所以$AB ⊥ CD$,则$\angle OHD = \angle BHD = 90°$。
在$\mathrm{Rt}\triangle BHD$中,$\cos \angle CDB = \frac{DH}{BD} = \frac{4}{5}$,$BD = 5$,所以$DH = 5 × \frac{4}{5} = 4$。
由勾股定理得$BH = \sqrt{BD^2 - DH^2} = \sqrt{5^2 - 4^2} = 3$。
设$\odot O$的半径为$r$,则$OB = OD = r$,$OH = OB - BH = r - 3$。
在$\mathrm{Rt}\triangle OHD$中,由勾股定理得$OH^2 + DH^2 = OD^2$,即$(r - 3)^2 + 4^2 = r^2$。
解得$r = \frac{25}{6}$。
故$\odot O$的半径为$\frac{25}{6}$。
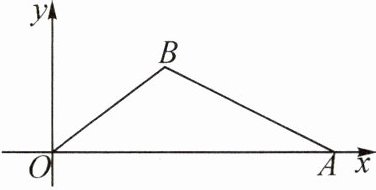
6. 如图,在平面直角坐标系中,$O$是原点,点$A$的坐标为$(10,0)$,点$B$在第一象限,$BO = 5$,$\sin \angle BOA = \dfrac{3}{5}$.
(1) 求点$B$的坐标;
(2) 求$\cos \angle BAO$的值.
]
答案:6.(1)过点B作BH⊥OA,垂足为H,则∠AHB = ∠OHB = 90°,所以$\sin∠BOA = \frac{BH}{BO} = \frac{3}{5}$.因为BO = 5,所以BH = 3,所以$OH = \sqrt{BO^2 - BH^2} = 4$,所以点B的坐标为(4,3).
(2)因为A(10,0),所以OA = 10.因为OH = 4,所以AH = OA - OH = 6.因为∠AHB = 90°,BH = 3,所以$AB = \sqrt{BH^2 + AH^2} = 3\sqrt{5}$,所以$\cos∠BAO = \frac{AH}{AB} = \frac{2\sqrt{5}}{5}$.
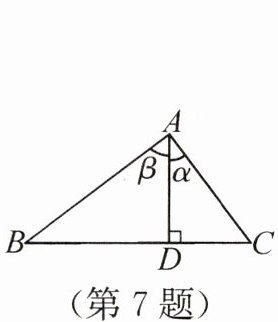
7. 新素养
推理能力 如图,在$Rt\triangle ABC$中,$\angle BAC = 90^{\circ}$,$AD ⊥ BC$,垂足为$D$.给出下列四个结论:①$\sin \alpha = \sin B$;②$\sin \beta = \sin C$;③$\sin B = \cos C$;④$\sin \alpha = \cos \beta$.其中正确的个数为(
D
)
A.$1$
B.$2$
C.$3$
D.$4$
答案:7.D
解析:
解:在$Rt\triangle ABC$中,$\angle BAC = 90^{\circ}$,$AD ⊥ BC$,则$\angle ADB=\angle ADC=90^{\circ}$。
$\angle \alpha +\angle \beta =90^{\circ}$,$\angle B +\angle C =90^{\circ}$,$\angle B +\angle \beta =90^{\circ}$,$\angle C +\angle \alpha =90^{\circ}$,故$\angle \alpha=\angle B$,$\angle \beta=\angle C$。
①$\sin\alpha=\sin B$,正确;
②$\sin\beta=\sin C$,正确;
③$\sin B=\cos(90^{\circ}-B)=\cos C$,正确;
④$\sin\alpha=\cos(90^{\circ}-\alpha)=\cos\beta$,正确。
正确的个数为4。
D
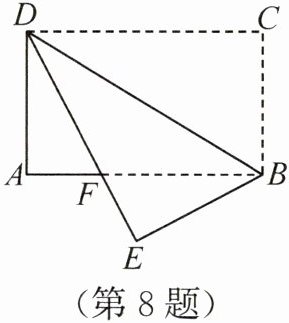
8. 如图,在矩形纸片$ABCD$中,$AB = 5$,$BC = 3$,将$\triangle BCD$沿$BD$折叠到$\triangle BED$的位置,$DE$交$AB$于点$F$,则$\cos \angle ADF$的值为(
C
)
A.$\dfrac{8}{17}$
B.$\dfrac{7}{15}$
C.$\dfrac{15}{17}$
D.$\dfrac{8}{15}$
答案:8.C
解析:
解:
∵ 四边形 $ABCD$ 为矩形,
∴ $AD = BC = 3$,$AB = CD = 5$,$\angle A = 90°$,$AB // CD$,
∴ $\angle CDB = \angle ABD$。
由折叠性质得:$\angle CDB = \angle FDB$,$DE = CD = 5$,
∴ $\angle FDB = \angle ABD$,
∴ $FB = FD$。
设 $AF = x$,则 $FB = FD = 5 - x$。
在 $Rt\triangle ADF$ 中,由勾股定理得:
$AD^2 + AF^2 = FD^2$,
即 $3^2 + x^2 = (5 - x)^2$,
解得 $x = \dfrac{8}{5}$,
∴ $FD = 5 - \dfrac{8}{5} = \dfrac{17}{5}$,
∴ $\cos \angle ADF = \dfrac{AD}{FD} = \dfrac{3}{\dfrac{17}{5}} = \dfrac{15}{17}$。
$\dfrac{15}{17}$
9. (2025·江苏连云港模拟)如图,在$Rt\triangle ABC$中,$\angle BAC = 90^{\circ}$,$\cos B = \dfrac{1}{4}$,$D$是边$BC$的中点,以$AD$为底边在其右侧作等腰三角形$ADE$,使$\angle ADE = \angle B$,连接$CE$,则$\dfrac{CE}{AD}$的值为(
D
)
A.$\dfrac{3}{2}$
B.$\sqrt{3}$
C.$\dfrac{\sqrt{15}}{2}$
D.$2$
答案:9.D解析:如图,设AC与DE交于点T,过点E作EH⊥BC于点H,则∠CHE = 90°.设BC = 4a.因为∠BAC = 90°,D是BC的中点,所以AD = BD = CD = $\frac{1}{2}$BC = 2a,所以∠BAD = ∠B.因为∠ADE = ∠B,所以∠BAD = ∠ADE,所以AB//DE,所以$\frac{CT}{AT} = \frac{CD}{BD} = 1$,∠CDE = ∠B,∠DTC = ∠BAC = 90°,所以AT = CT,DE⊥AC,所以DE垂直平分AC,所以AE = CE.因为AE = DE,所以DE = CE,所以$DH = CH = \frac{1}{2}CD = a$,∠DCE = ∠CDE,所以∠DCE = ∠B,所以$\cos∠DCE = \cos B = \frac{1}{4}$.因为$\cos∠DCE = \frac{CH}{CE}$,所以$\frac{CH}{CE} = \frac{1}{4}$,所以CE = 4a,所以$\frac{CE}{AD} = 2$.