1. (2025·江苏苏州期末·3分)如图,在矩形 $ABCD$ 中,$AB = 3$,分别以 $A$,$C$ 两点为圆心,大于 $\frac{1}{2}AC$ 的长为半径画弧,两弧相交于 $M$,$N$ 两点,作直线 $MN$,分别交 $AD$,$BC$ 于 $E$,$F$ 两点,连接 $AF$,$CE$.若 $EF = BF + DE$,则边 $BC$ 的长为(
B
)
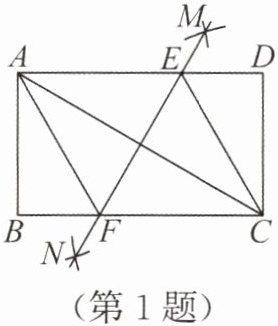
A.$\sqrt{12}$
B.$\sqrt{27}$
C.$6$
D.$\sqrt{45}$
(第1题)
答案:1. B
解析:
证明:
∵四边形$ABCD$是矩形,$\therefore AD// BC$,$AD=BC$,$AB=CD=3$,$\angle B=90°$。
由作图知,$MN$是$AC$的垂直平分线,$\therefore AF=CF$,$AE=CE$,$OA=OC$。
$\because AD// BC$,$\therefore \angle EAO=\angle FCO$。
在$\triangle AOE$和$\triangle COF$中,
$\{\begin{array}{l} \angle EAO=\angle FCO \\ OA=OC \\ \angle AOE=\angle COF \end{array} $,
$\therefore \triangle AOE\cong \triangle COF(ASA)$,$\therefore AE=CF$,$OE=OF$。
$\because AF=CF$,$AE=CF$,$\therefore AE=AF=CF=CE$,
$\therefore$四边形$AFCE$是菱形,$\therefore EF=2OE$,$AF=CF$。
设$BF=x$,$BC=AD=y$,则$CF=AF=y-x$。
在$Rt\triangle ABF$中,$AB^2+BF^2=AF^2$,即$3^2+x^2=(y-x)^2$,
化简得$9+x^2=y^2-2xy+x^2$,$\therefore y^2-2xy=9$ ①。
$\because AE=CF=y-x$,$\therefore DE=AD-AE=y-(y-x)=x$。
$\because EF=BF+DE$,$\therefore EF=x+x=2x$。
$\because$四边形$AFCE$是菱形,$\therefore AC⊥ EF$,$OA=\frac{1}{2}AC$,$OE=\frac{1}{2}EF=x$。
在$Rt\triangle AOE$中,$OA^2+OE^2=AE^2$,即$OA^2+x^2=(y-x)^2$,$\therefore OA^2=(y-x)^2-x^2=y^2-2xy$。
由①得$OA^2=9$,$\therefore OA=3$,$\therefore AC=2OA=6$。
在$Rt\triangle ABC$中,$AB^2+BC^2=AC^2$,即$3^2+y^2=6^2$,
$\therefore y^2=36-9=27$,$\therefore y=\sqrt{27}$(负值舍去)。
$\therefore BC=\sqrt{27}$。
答案:$\sqrt{27}$
2. (3分)新素养
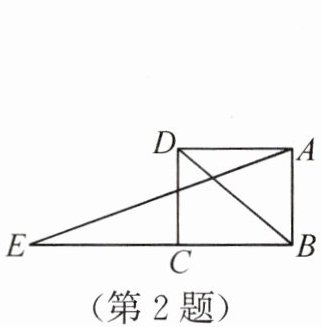
运算能力 如图,延长矩形 $ABCD$ 的边 $BC$ 至点 $E$,使 $CE = BD$,连接 $AE$.若 $\angle DBC = 40^{\circ}$,则 $\angle E$ 的度数为
20°
.
答案:2. 20°
解析:
解:连接AC。
∵四边形ABCD是矩形,
∴AC=BD,∠BCD=90°。
∵CE=BD,
∴AC=CE,
∴∠E=∠CAE。
∵∠DBC=40°,
∴∠ACB=∠DBC=40°(矩形对角线相等且互相平分)。
∵∠ACB=∠E+∠CAE=2∠E,
∴∠E=20°。
20°
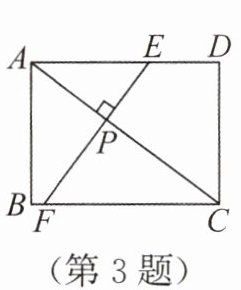
3. (2025·江苏南京期末·3分)上分点二 如图,在矩形 $ABCD$ 中,$AB = 3$,$AD = 4$,动点 $P$ 在对角线 $AC$ 上,过点 $P$ 作 $AC$ 的垂线分别交 $AD$,$BC$ 于 $E$,$F$ 两点,则 $EF =$
$\frac{15}{4}$
.
答案:$3. \frac{15}{4}$
解析:
解:在矩形$ABCD$中,$AB = 3$,$AD = 4$,则$BC = AD = 4$,$CD = AB = 3$,$\angle ADC = 90°$。
在$Rt\triangle ADC$中,$AC=\sqrt{AD^2 + CD^2}=\sqrt{4^2 + 3^2}=5$。
设$AP = x$,则$PC = 5 - x$。
因为$EF⊥ AC$,所以$\angle APE=\angle CPF = 90°$。
又因为$AD// BC$,所以$\angle EAP=\angle FCP$。
故$\triangle APE∼\triangle CPF$,则$\frac{EP}{FP}=\frac{AP}{CP}=\frac{x}{5 - x}$。
在$Rt\triangle APE$中,$\tan\angle EAP=\frac{EP}{AP}=\frac{CD}{AD}=\frac{3}{4}$,所以$EP=\frac{3}{4}x$。
在$Rt\triangle CPF$中,$\tan\angle FCP=\frac{FP}{CP}=\frac{AB}{BC}=\frac{3}{4}$,所以$FP=\frac{3}{4}(5 - x)$。
因此$EF=EP + FP=\frac{3}{4}x+\frac{3}{4}(5 - x)=\frac{15}{4}$。
$\frac{15}{4}$
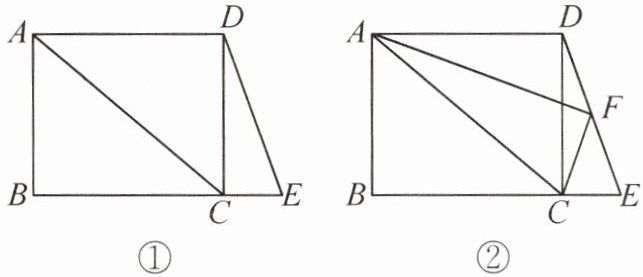
4. (8分)已知四边形 $ABCD$ 是矩形,$E$ 是 $BC$ 延长线上一点,连接 $AC$,$DE$,$BE = AC$.
(1) 如图①,若 $\angle ACB = 40^{\circ}$,求 $\angle E$ 的度数;
(2) 如图②,若 $F$ 是 $DE$ 的中点,连接 $AF$,$CF$,求证:$AF⊥ FC$.
答案:4. (1) 连接 BD,交 AC 于点 O. 因为四边形 ABCD 是矩形,所以 BD = AC,OB = OC,即 ∠DBE = ∠ACB. 又 ∠ACB = 40°,所以 ∠DBE = 40°. 又 BE = AC,所以 BE = BD,即 ∠E = ∠BDE. 又 ∠E + ∠BDE + ∠DBE = 180°,所以$ ∠E = \frac{1}{2}(180° - ∠DBE) = 70°.$
(2) 延长 CF,交 AD 的延长线于点 G. 因为四边形 ABCD 为矩形,所以 AD = BC,AD // BC,即 AG // BE. 所以 ∠G = ∠ECF,∠GDF = ∠CEF. 又 F 是 DE 的中点,所以 DF = EF. 所以 △DFG ≌ △EFC (AAS). 所以 DG = EC,FG = FC,即 F 是 CG 的中点,AD + DG = BC + EC. 所以 AG = BE. 又 BE = AC,所以 AG = AC. 所以 AF ⊥ CG,即 AF ⊥ FC.
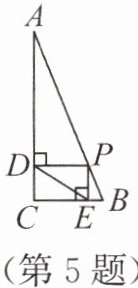
5. (2024·西藏·3分)上分点一 如图,在 $Rt\triangle ABC$ 中,$\angle C = 90^{\circ}$,$AC = 12$,$BC = 5$,$P$ 是边 $AB$ 上任意一点,过点 $P$ 分别作 $PD⊥ AC$,$PE⊥ BC$,垂足分别为 $D$,$E$,连接 $DE$,则 $DE$ 的长的最小值是(
B
)
A.$\frac{13}{2}$
B.$\frac{60}{13}$
C.$\frac{12}{5}$
D.$\frac{30}{13}$
答案:5. B
解析:
解:在$Rt\triangle ABC$中,$\angle C=90^{\circ}$,$AC=12$,$BC=5$,
由勾股定理得$AB=\sqrt{AC^{2}+BC^{2}}=\sqrt{12^{2}+5^{2}}=13$。
设$PD=EC=x$,$PE=DC=y$,
$\because PD⊥ AC$,$PE⊥ BC$,$\angle C=90^{\circ}$,
$\therefore$四边形$CDPE$是矩形,$\therefore DE=CP$。
$\because PD// BC$,$\therefore \triangle ADP\backsim \triangle ACB$,
$\therefore \frac{AD}{AC}=\frac{PD}{BC}$,即$\frac{12 - y}{12}=\frac{x}{5}$,$\therefore 5(12 - y)=12x$,
$\therefore y=\frac{60 - 12x}{5}$。
在$Rt\triangle CDP$中,$CP=\sqrt{y^{2}+x^{2}}=\sqrt{x^{2}+(\frac{60 - 12x}{5})^{2}}$,
$=\sqrt{\frac{25x^{2}+144x^{2}-1440x + 3600}{25}}=\sqrt{\frac{169x^{2}-1440x + 3600}{25}}$,
当$x=-\frac{b}{2a}=\frac{1440}{2×169}=\frac{720}{169}$时,$CP$最小,
$CP_{\mathrm{min}}=\sqrt{\frac{169×(\frac{720}{169})^{2}-1440×\frac{720}{169}+3600}{25}}=\frac{60}{13}$,
$\therefore DE$的最小值为$\frac{60}{13}$。
答案:B