7. (3 分)
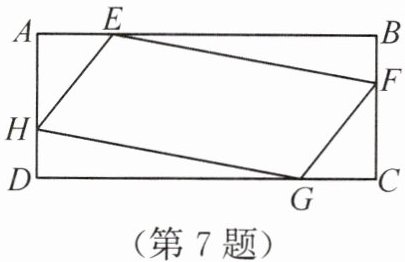
上分点三 如图,在长方形 ABCD 中,AB=12,BC=5,E,F,G,H 四点分别在长方形 ABCD 的各边上,且 AE=CG,BF=DH,则四边形 EFGH 周长的最小值为(
B
)
A.13
B.26
C.17
D.34
答案:7. B
解析:
证明:设 $AE = CG = a$,$BF = DH = b$,则 $AH = 5 - b$,$BE = 12 - a$,$CF = 5 - b$,$DG = 12 - a$。
在 $Rt\triangle AEH$ 中,$EH = \sqrt{AE^2 + AH^2} = \sqrt{a^2 + (5 - b)^2}$;
在 $Rt\triangle BEF$ 中,$EF = \sqrt{BE^2 + BF^2} = \sqrt{(12 - a)^2 + b^2}$;
同理,$FG = \sqrt{CG^2 + CF^2} = \sqrt{a^2 + (5 - b)^2} = EH$,
$GH = \sqrt{DG^2 + DH^2} = \sqrt{(12 - a)^2 + b^2} = EF$。
四边形 $EFGH$ 周长 $C = 2(EH + EF) = 2[\sqrt{a^2 + (5 - b)^2} + \sqrt{(12 - a)^2 + b^2}]$。
作点 $E$ 关于 $AB$ 的对称点 $E'$($AE' = AE = a$),点 $F$ 关于 $BC$ 的对称点 $F'$($CF' = CF = 5 - b$),则 $E'H = EH$,$F'G = FG$,但更简便的是通过平移转化:将 $EH$ 平移使 $H$ 与 $D$ 重合,$EF$ 平移使 $F$ 与 $C$ 重合,此时 $EH + EF$ 转化为点 $(a, 5 - b)$ 到 $(0, 0)$ 与 $(12, b)$ 的距离之和,其最小值为矩形对角线长 $\sqrt{12^2 + 5^2} = 13$。
故周长最小值 $C = 2 × 13 = 26$。
答案:B
8. (3 分)如图,在△ABC 中,∠BAC=90°,AB=4,AC=6,D,E 分别是 BC,AD 的中点,AF//BC,交 CE 的延长线于点 F,连接 BF,则四边形 AFBD 的面积为
12
.

答案:8. 12
解析:
解:在△ABC中,∠BAC=90°,AB=4,AC=6,
∴S△ABC=$\frac{1}{2}$×AB×AC=$\frac{1}{2}$×4×6=12。
∵D是BC的中点,
∴S△ABD=$\frac{1}{2}$S△ABC=6。
∵AF//BC,
∴∠AFE=∠DCE。
∵E是AD的中点,
∴AE=DE。
在△AFE和△DCE中,
$\{\begin{array}{l}∠AFE=∠DCE\\∠AEF=∠DEC\\AE=DE\end{array} $,
∴△AFE≌△DCE(AAS),
∴AF=DC。
∵D是BC的中点,
∴BD=DC,
∴AF=BD。
∵AF//BD,
∴四边形AFBD是平行四边形,
∴S四边形AFBD=2S△ABD=2×6=12。
故答案为12。
9. (3 分)亮点原创 如图,在△ABC 中,∠BAC=105°. 若△ABD,△ACE,△BCF 都是等边三角形,AE=√8,AB=4,则四边形 AEFD 的面积为
8
.

答案:9. 8 解析:过点E作EG⊥AD,交DA的延长线于点G,则∠AEG + ∠EAG = 90°. 因为△ABD,△ACE,△BCF 都是等边三角形,所以AB = BD = AD,AC = AE = CE,BC = CF = BF,∠ACE = ∠BCF = ∠ABD = ∠CBF = ∠BAD = ∠CAE = 60°. 所以∠BCF - ∠ACF = ∠ACE - ∠ACF,∠CBF - ∠ABF = ∠ABD - ∠ABF,即∠ACB = ∠ECF,∠ABC = ∠DBF. 所以△ABC≅△DBF≅△EFC(SAS). 所以DF = AC,AB = EF,即DF = AE,AD = EF. 所以四边形AEFD是平行四边形. 又∠BAC = 105°,所以∠EAG = ∠BAD + ∠BAC + ∠CAE - 180° = 45°,
即∠AEG = ∠EAG. 所以AG = EG. 在Rt△AEG中,$AE = \sqrt{8},$由勾股定理,得AG² + EG² = AE²,所以EG = 2. 又AB = 4,所以AD = 4. 所以四边形AEFD的面积为AD · EG = 8.
10. (8
分)上分点
四 新素养
推理能力 如图,在□ABCD 中,AC,BD 相交于点 O,AE⊥BD 于点 E,CF⊥BD 于点 F,BG⊥AC 于点 G,DH⊥AC 于点 H,连接 EH,HF,FG,GE,则四边形 EHFG 是平行四边形吗?请说明理由.
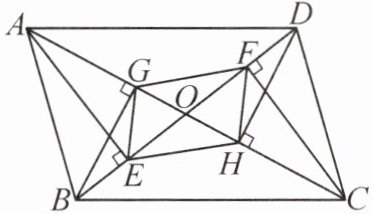
答案:10. 四边形EHFG是平行四边形. 理由如下:因为四边形ABCD是平行四边形,所以OA = OC,OB = OD. 又AE⊥BD,CF⊥BD,BG⊥AC,DH⊥AC,所以∠AEO = ∠CFO = ∠BGO = ∠DHO = 90°. 又∠BOG = ∠DOH,∠AOE = ∠COF,所以△BOG ≅ △DOH (AAS),△AOE ≅ △COF (AAS). 所以OG = OH,OE = OF. 所以四边形EHFG是平行四边形.
11. (10 分)如图,在△ABC 中,AB=AC,点 D 在 BC 上,连接 AD,作∠ADE=∠ABC,以 DE 为底作等腰三角形 ADE,连接 CE,过点 E 作 EM//BC,交 CA 的延长线于点 M,连接 BM.
(1)求证:△BAD≌△CAE;
(2)若∠ABC=30°,求∠MEC 的度数;
(3)求证:四边形 MBDE 是平行四边形.
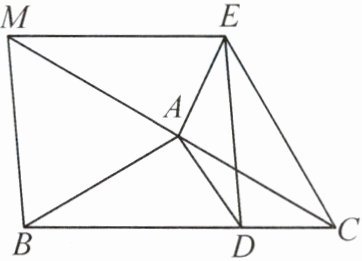
答案:11. (1)因为AB = AC,AD = AE,所以∠ABC = ∠ACB,∠ADE = ∠AED. 又∠ADE = ∠ABC,∠ABC + ∠ACB + ∠BAC = 180°,∠ADE + ∠AED + ∠DAE = 180°,所以∠BAC = ∠DAE. 所以∠BAC - ∠CAD = ∠DAE - ∠CAD,即∠BAD = ∠CAE. 所以△BAD ≅ △CAE(SAS).
(2)由(1),得△BAD ≅ △CAE,∠ABC = ∠ACB,所以∠ABD = ∠ACE,即∠ABC = ∠MCE. 又EM//BC,所以∠ACB = ∠CME,即∠CME = ∠ABC. 又∠ABC = 30°,所以∠CME = ∠MCE = 30°. 又∠MEC + ∠CME + ∠MCE = 180°,所以∠MEC = 120°.
(3)由(1)(2),得△BAD ≅ △CAE,∠CME = ∠MCE,所以BD = CE,ME = CE,即BD = ME. 又EM//BC,所以四边形MBDE是平行四边形.