8. 在一个不透明的口袋中装有4个红球和若干白球,它们除颜色外其他完全相同,通过多次摸球试验后发现,摸到红球的频率稳定在25%附近,则口袋中白球大约有
12
个.
答案:8.12
解析:
设口袋中白球有$x$个,球的总数为$(4 + x)$个。
因为摸到红球的频率稳定在$25\%$附近,所以摸到红球的概率为$25\%=\frac{1}{4}$。
根据概率公式可得:$\frac{4}{4 + x}=\frac{1}{4}$
解得:$4×4 = 4 + x$,$16 = 4 + x$,$x = 12$
12
9. 已知$(a + b)(a + b - 6) + 9 = 0$,且$a^{2}b^{2} - 4ab + 4 = 0$,则$a - b =$
±1
.
答案:9.±1
解析:
设$x = a + b$,则方程$(a + b)(a + b - 6) + 9 = 0$可化为$x(x - 6) + 9 = 0$,即$x^2 - 6x + 9 = 0$,$(x - 3)^2 = 0$,解得$x = 3$,所以$a + b = 3$。
设$y = ab$,方程$a^2b^2 - 4ab + 4 = 0$可化为$y^2 - 4y + 4 = 0$,即$(y - 2)^2 = 0$,解得$y = 2$,所以$ab = 2$。
$(a - b)^2 = (a + b)^2 - 4ab = 3^2 - 4×2 = 9 - 8 = 1$,则$a - b = ±1$。
±1
10. 若关于$x$的分式方程$\frac{x - a}{x + 1} = a$无解,则$a$的值为
±1
.
答案:10.±1
解析:
解:方程两边同乘$x + 1$,得$x - a = a(x + 1)$,
整理得$(1 - a)x = 2a$。
当$1 - a = 0$,即$a = 1$时,方程无解。
当$1 - a \neq 0$时,$x = \frac{2a}{1 - a}$,
若$x = -1$,则原方程无解,
即$\frac{2a}{1 - a} = -1$,解得$a = -1$。
综上,$a = \pm1$。
11. 已知$a$,$b$均为正整数,且$\sqrt{a} + \sqrt{b} = \sqrt{27}$,则$\frac{b}{a}$的值为
$\frac{1}{4}$或4
.
答案:11.$\frac{1}{4}$或4
解析:
解:$\sqrt{27} = 3\sqrt{3}$,设$\sqrt{a} = m\sqrt{3}$,$\sqrt{b} = n\sqrt{3}$,其中$m$,$n$为正整数。
则$m\sqrt{3} + n\sqrt{3} = 3\sqrt{3}$,即$(m + n)\sqrt{3} = 3\sqrt{3}$,所以$m + n = 3$。
正整数解为:
当$m = 1$,$n = 2$时,$\sqrt{a} = \sqrt{3}$,$a = 3$;$\sqrt{b} = 2\sqrt{3} = \sqrt{12}$,$b = 12$,$\frac{b}{a} = \frac{12}{3} = 4$。
当$m = 2$,$n = 1$时,$\sqrt{a} = 2\sqrt{3} = \sqrt{12}$,$a = 12$;$\sqrt{b} = \sqrt{3}$,$b = 3$,$\frac{b}{a} = \frac{3}{12} = \frac{1}{4}$。
综上,$\frac{b}{a}$的值为$\frac{1}{4}$或$4$。
12. 如图,四边形$ABCD$是菱形,$O$是对角线的交点,过点$O$的三条直线将菱形分成空白和阴影部分. 若菱形$ABCD$的两条对角线的长分别为$2\sqrt{2}$cm和$\sqrt{6}$cm,则图中阴影部分的面积为
$\sqrt{3}$
$\mathrm{cm}^{2}$.

答案:12.$\sqrt{3}$
解析:
解:菱形的面积为$\frac{1}{2} × 2\sqrt{2} × \sqrt{6} = \sqrt{12} = 2\sqrt{3}\, \mathrm{cm}^2$。
因为菱形的对角线互相平分且中心对称,过点$O$的直线将菱形分成的阴影部分面积为菱形面积的一半,所以阴影部分面积为$\frac{1}{2} × 2\sqrt{3} = \sqrt{3}\, \mathrm{cm}^2$。
$\sqrt{3}$
13. 新素养
运算能力 已知$m$,$n$,$p$都是正数,且$\frac{p}{m + n} + \frac{n}{m + p} + \frac{m}{n + p} = 2$,$\frac{1}{m + n} + \frac{1}{m + p} + \frac{1}{n + p} = \frac{4}{5}$,则$m + n + p =$
$\frac{25}{4}$
.
答案:13.$\frac{25}{4}$ 解析:设m + n + p = k,则p = k - (m + n),n = k - (p + m),m = k - (n + p)。所以$\frac{p}{m + n}$ + $\frac{n}{m + p}$ + $\frac{m}{n + p}$ = $\frac{k - (m + n)}{m + n}$ + $\frac{k - (m + p)}{m + p}$ + $\frac{k - (n + p)}{n + p}$ = $\frac{k}{m + n}$ + $\frac{k}{m + p}$ + $\frac{k}{n + p}$ - 3。又$\frac{p}{m + n}$ + $\frac{n}{m + p}$ + $\frac{m}{n + p}$ = 2,所以$\frac{k}{m + n}$ + $\frac{k}{m + p}$ + $\frac{k}{n + p}$ - 3 = 2,即k·($\frac{1}{m + n}$ + $\frac{1}{m + p}$ + $\frac{1}{n + p}$) = 5。又$\frac{1}{m + n}$ + $\frac{1}{m + p}$ + $\frac{1}{n + p}$ = $\frac{4}{5}$,所以$\frac{4}{5}$k = 5,解得k = $\frac{25}{4}$。所以m + n + p = $\frac{25}{4}$。
解析:
设$m + n + p = k$,则$p = k - (m + n)$,$n = k - (m + p)$,$m = k - (n + p)$。
$\begin{aligned}\frac{p}{m + n} + \frac{n}{m + p} + \frac{m}{n + p}&=\frac{k - (m + n)}{m + n} + \frac{k - (m + p)}{m + p} + \frac{k - (n + p)}{n + p}\\&=\frac{k}{m + n} - 1 + \frac{k}{m + p} - 1 + \frac{k}{n + p} - 1\\&=k(\frac{1}{m + n} + \frac{1}{m + p} + \frac{1}{n + p}) - 3\end{aligned}$
已知$\frac{p}{m + n} + \frac{n}{m + p} + \frac{m}{n + p} = 2$,$\frac{1}{m + n} + \frac{1}{m + p} + \frac{1}{n + p} = \frac{4}{5}$,代入上式得:
$k × \frac{4}{5} - 3 = 2$
解得:
$\frac{4}{5}k = 5 \implies k = \frac{25}{4}$
$\frac{25}{4}$
14. (2025·江苏宿迁期末)如图,在$\triangle ABC$中,$\angle A = 60^{\circ}$,$AC > AB > 2$,$D$,$E$两点分别在边$AB$,$AC$上,且$BD = CE = 2$,连接$DE$,$M$是$DE$的中点,$N$是$BC$的中点,则线段$MN$的长为
$\sqrt{3}$
.
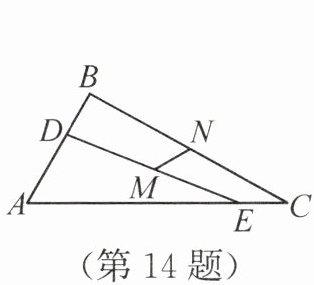
答案:14.$\sqrt{3}$ 解析:如图,过点C作CH//AB,连接DN 并延长,交CH 于点H,连接EH,过点C作CJ⊥EH于点J,则∠B = ∠NCH,∠A + ∠ECH = 180°。又∠A = 60°,所以∠ECH = 180° - ∠A = 120°。因为N是BC的中点,所以BN = CN。又∠DNB = ∠HNC,所以△DNB ≌ △HNC(ASA)。所以BD = CH,DN = HN。所以N是DH的中点。又M是DE的中点,所以MN是△DEH的中位线,即MN = $\frac{1}{2}$EH。因为BD = CE = 2,所以CE = CH = 2。所以∠CEJ = ∠CHJ,EH = 2EJ,即MN = EJ。又∠CEJ + ∠CHJ + ∠ECH = 180°,所以∠CEJ = $\frac{1}{2}$(180° - ∠ECH) = 30°。所以CJ = $\frac{1}{2}$EC = 1。在Rt△CEJ 中,由勾股定理,得EJ = $\sqrt{EC^{2}-CJ^{2}}$ = $\sqrt{3}$。所以MN = $\sqrt{3}$。

15. (15分)计算与解方程:
(1)$(\frac{a^{2}}{a - 3} + \frac{9}{3 - a}) ÷ \frac{a + 3}{a}$;
(2)$(14\sqrt{54} - 8\sqrt{24} - \sqrt{216}) ÷ 2\sqrt{6} × \frac{1}{\sqrt{6}}$;
(3)$\frac{x}{x - 1} - \frac{3}{(x - 1)(x + 2)} = 1$.
答案:15.(1)原式 = $\frac{(a + 3)(a - 3)}{a - 3}$·$\frac{a}{a + 3}$ = a。
(2)原式 = (42$\sqrt{6}$ - 16$\sqrt{6}$ - 6$\sqrt{6}$)×$\frac{1}{2\sqrt{6}}$×$\frac{1}{\sqrt{6}}$ = 20$\sqrt{6}$×$\frac{1}{12}$ = $\frac{5\sqrt{6}}{3}$。
(3)无解(x = 1是增根)。