9. (3 分)已知 $ m^2 + n^2 = 2m - 6n - 10 $,则代数式 $\frac{2}{m + n} - \frac{m - n}{m - 2} ÷ (m + 2 - \frac{n^2 - 4}{m - 2})$ =
$-\frac{1}{2}$
.
答案:9. $-\frac{1}{2}$
解析:
由$m^2 + n^2 = 2m - 6n - 10$,得$(m - 1)^2 + (n + 3)^2 = 0$,则$m = 1$,$n = -3$。
原式$=\frac{2}{m + n} - \frac{m - n}{m - 2} ÷ (\frac{(m + 2)(m - 2) - (n^2 - 4)}{m - 2})$
$=\frac{2}{m + n} - \frac{m - n}{m - 2} ÷ \frac{m^2 - n^2}{m - 2}$
$=\frac{2}{m + n} - \frac{m - n}{m - 2} · \frac{m - 2}{(m + n)(m - n)}$
$=\frac{2}{m + n} - \frac{1}{m + n}$
$=\frac{1}{m + n}$
将$m = 1$,$n = -3$代入,得$\frac{1}{1 + (-3)} = -\frac{1}{2}$。
$-\frac{1}{2}$
10. (3 分)如图,在矩形 $ ABCD $ 中,$ AB = 1,BC = 7 $,将矩形 $ ABCD $ 绕点 $ C $ 按顺时针方向旋转 $ 90° $ 得到矩形 $ A'B'CD' $,连接 $ BD,B'D' $,$ E,F $ 分别是 $ BD,B'D' $ 的中点,则 $ EF $ 的长为
$5$
.
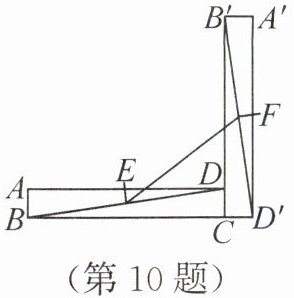
答案:10. $5$
11. (3 分)新趋势
传统文化 2025 年春晚吉祥物“巳(sì)升升”,是从中华传统文化中寻找的灵感,整体造型参考甲骨文中的“巳”字,其形象既憨态可掬,又富有古意.某商店销售 $ A,B $ 两款“巳升升”吉祥物,每个 $ A $ 款吉祥物的价格比每个 $ B $ 款吉祥物的价格高 20 元.若顾客花 800 元购买 $ A $ 款吉祥物的数量与花 600 元购买 $ B $ 款吉祥物的数量相同,则每个 $ A $ 款吉祥物的价格为
$80$
元.
答案:11. $80$
解析:
设每个B款吉祥物的价格为$x$元,则每个A款吉祥物的价格为$(x + 20)$元。
根据题意,得$\dfrac{800}{x + 20} = \dfrac{600}{x}$。
方程两边同乘$x(x + 20)$,得$800x = 600(x + 20)$。
解得$x = 60$。
经检验,$x = 60$是原分式方程的解,且符合题意。
则$x + 20 = 60 + 20 = 80$。
80
12. (3 分)已知 $ a = \frac{1}{2 + \sqrt{3}},b = \frac{1}{2 - \sqrt{3}} $,则 $ 3a^2 + 11ab - 3b^2 $ 的值是
$-24\sqrt{3}+11$
.
答案:12. $-24\sqrt{3}+11$
解析:
解:$a = \frac{1}{2 + \sqrt{3}} = 2 - \sqrt{3}$,$b = \frac{1}{2 - \sqrt{3}} = 2 + \sqrt{3}$,
$a + b = 4$,$a - b = -2\sqrt{3}$,$ab = 1$,
$3a^2 + 11ab - 3b^2 = 3(a^2 - b^2) + 11ab = 3(a + b)(a - b) + 11ab$,
代入得:$3×4×(-2\sqrt{3}) + 11×1 = -24\sqrt{3} + 11$。
$-24\sqrt{3} + 11$
13. (3 分)如图,在菱形 $ ABCD $ 中,$ M,N $ 分别是边 $ AD,BC $ 上的动点.若 $ MN $ 的长的最大值为 $\sqrt{65}$,最小值为 4,则菱形 $ ABCD $ 的面积为
$\frac{130}{7}$
.

答案:13. $\frac{130}{7}$ 解析:如图,过点$B$作$BE⊥ AD$,交$DA$的延长线于点$E$。当点$M$运动到点$D$处,点$N$运动到点$B$处时,$MN$的长最大,所以$BD=\sqrt{65}$。当$MN⊥ AD$时,$MN$的长最小,所以$BE = 4$。在$\mathrm{Rt}\triangle DBE$中,由勾股定理,得$DE=\sqrt{BD^{2}-BE^{2}} = 7$。因为四边形$ABCD$是菱形,所以$AD = AB = BC$。设$AD = x$,则$AB = x$,$AE = 7 - x$。在$\mathrm{Rt}\triangle ABE$中,由勾股定理,得$BE^{2}+AE^{2}=AB^{2}$,所以$4^{2}+(7 - x)^{2}=x^{2}$,解得$x=\frac{65}{14}$,则$AD=\frac{65}{14}$。所以菱形$ABCD$的面积为$AD· BE=\frac{65}{14}×4=\frac{130}{7}$。
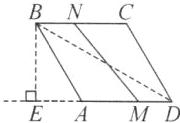
14. (4 分)如图,$□ ABCD$ 的顶点 $ C $ 在等边三角形 $ BEF $ 的边 $ BF $ 上,点 $ E $ 在 $ AB $ 的延长线上,$ G $ 为 $ DE $ 的中点,连接 $ CG $.若 $ AD = 3,AB = CF = 2 $,则 $ CG $ 的长为
$\frac{3}{2}$
.

答案:14. $\frac{3}{2}$ 解析:延长$CG$交$BE$于点$H$,则$\angle DGC=\angle EGH$。又四边形$ABCD$是平行四边形,$AB = 2$,$AD =3$,所以$AB// CD$,$CD = AB = 2$,$BC = AD = 3$。又点$E$在$AB$的延长线上,所以$CD// EH$。所以$\angle CDG=\angle HEG$。又$G$为$DE$的中点,所以$DG = EG$。所以$\triangle DCG\cong\triangle EHG(ASA)$。所以$EH = DC = 2$,$HG = CG=\frac{1}{2}CH$。又$CF = 2$,所以$BF = BC + CF = 5$。又$\triangle BEF$是等边三角形,所以$\angle EBF = 60^{\circ}$,$BE = BF = 5$。所以$BH = BE - EH = 3$。则$BC = BH$。所以$\triangle BCH$是等边三角形。所以$CH = BH = 3$,即$CG=\frac{3}{2}$。
解析:
解:延长$CG$交$BE$于点$H$。
因为四边形$ABCD$是平行四边形,$AD = 3$,$AB = 2$,所以$AB// CD$,$CD = AB = 2$,$BC = AD = 3$。
因为点$E$在$AB$的延长线上,所以$CD// EH$,则$\angle CDG=\angle HEG$。
因为$G$为$DE$的中点,所以$DG = EG$。
在$\triangle DCG$和$\triangle EHG$中,$\{\begin{array}{l}\angle CDG=\angle HEG\\ DG = EG\\ \angle DGC=\angle EGH\end{array} $,所以$\triangle DCG\cong\triangle EHG(ASA)$。
所以$EH = DC = 2$,$HG = CG=\frac{1}{2}CH$。
因为$CF = 2$,所以$BF = BC + CF = 3 + 2 = 5$。
因为$\triangle BEF$是等边三角形,所以$BE = BF = 5$,$\angle EBF = 60^{\circ}$。
所以$BH = BE - EH = 5 - 2 = 3$,则$BC = BH = 3$。
所以$\triangle BCH$是等边三角形,$CH = BH = 3$。
因此$CG=\frac{1}{2}CH=\frac{3}{2}$。
$\frac{3}{2}$
15. (2025·江苏南京期末·4 分)若关于 $ x $ 的分式方程 $\frac{x - a}{x - 1} - \frac{3}{x} = 1$ 无解,则 $ a =$
$1$或$-2$
.
答案:15. $1$或$-2$ 解析:对于分式方程$\frac{x - a}{x - 1}-\frac{3}{x}=1$,化简,得$(a + 2)x = 3$。因为该分式方程无解,所以有$(a + 2)x = 3$无解或分式方程有增根。当$(a + 2)x = 3$无解时,$a + 2 = 0$,解得$a=-2$;当分式方程有增根时,$x = 1$或$x = 0$。当$x = 1$时,$a + 2 = 3$,解得$a = 1$;当$x = 0$时,整式方程不成立。综上,$a$的值为$1$或$-2$。
解析:
方程两边同乘$x(x - 1)$,得$x(x - a)-3(x - 1)=x(x - 1)$,化简得$(a + 2)x=3$。
当$a + 2 = 0$,即$a=-2$时,方程$(a + 2)x = 3$无解,原分式方程无解;
当$a + 2\neq0$时,$x=\frac{3}{a + 2}$。若原分式方程有增根,则$x(x - 1)=0$,即$x = 0$或$x = 1$。
当$x = 1$时,$\frac{3}{a + 2}=1$,解得$a = 1$;当$x = 0$时,$\frac{3}{a + 2}=0$,无解。
综上,$a = 1$或$a=-2$。
16. (4 分)如图,菱形 $ ABCD $ 的边长为 5,$\angle BAD = 60°$,对角线 $ AC $ 上有两个动点 $ E,F $(点 $ E $ 在点 $ F $ 的左侧),连接 $ DE,BF $.若 $ EF = 2 $,则 $ DE + BF $ 的最小值为
$\sqrt{29}$
.

答案:16. $\sqrt{29}$ 解析:连接$BD$。因为四边形$ABCD$是边长为$5$的菱形,所以$AB = AD = 5$,$AC⊥ BD$。因为$\angle BAD = 60^{\circ}$,所以$\triangle ADB$是等边三角形,即$BD = AB = 5$。以$DE$,$EF$为边作平行四边形$DEFG$,连接$BG$,则$DG// AC$,$DG = EF$,$FG = DE$,即$BD⊥ DG$。所以$\angle BDG = 90^{\circ}$。又$EF = 2$,所以$DG = 2$。在$\mathrm{Rt}\triangle BDG$中,由勾股定理,得$BG=\sqrt{DG^{2}+BD^{2}}=\sqrt{29}$。所以$DE + BF = FG + BF\geqslant BG$,即当$B$,$F$,$G$三点共线时,$DE + BF$取最小值,且最小值为$BG$的长。所以$DE + BF$的最小值为$\sqrt{29}$。
解析:
证明:连接$BD$。
∵四边形$ABCD$是菱形,边长为$5$,
∴$AB = AD = 5$,$AC ⊥ BD$。
∵$\angle BAD = 60°$,
∴$\triangle ADB$是等边三角形,$BD = AB = 5$。
以$DE$,$EF$为边作平行四边形$DEFG$,连接$BG$,
则$DG // AC$,$DG = EF = 2$,$FG = DE$。
∵$AC ⊥ BD$,$DG // AC$,
∴$BD ⊥ DG$,即$\angle BDG = 90°$。
在$\mathrm{Rt}\triangle BDG$中,由勾股定理得:
$BG = \sqrt{DG^2 + BD^2} = \sqrt{2^2 + 5^2} = \sqrt{29}$。
∵$DE + BF = FG + BF \geq BG$(当且仅当$B$,$F$,$G$三点共线时取等号),
∴$DE + BF$的最小值为$\sqrt{29}$。
$\sqrt{29}$
17. (4 分)已知 $ a,b $ 为互不相等的非零实数,满足 $ a^2(b + c) = b^2(c + a) = 8 $,则 $ c^2(a + b) + 2abc =$
$-8$
.
答案:17. $-8$ 解析:因为$a^{2}(b + c)=b^{2}(c + a)=8$,所以$a^{2}b + a^{2}c = b^{2}c + ab^{2}$,即$ab(a - b)+c(a^{2}-b^{2})=0$。所以$(a - b)(ab + ac + bc)=0$。又$a\neq b$,所以$ab + ac + bc = 0$,即$ab + ac=-bc$。所以$a^{2}(b + c)=a(ab + ac)=-abc = 8$,即$abc = - 8$。所以$c^{2}(a + b)+2abc = ac^{2}+abc + bc^{2}+abc = c(ac + ab)+bc^{2}+abc=-bc^{2}+bc^{2}+abc = abc = - 8$。
18. (5 分)如图,正方形 $ ABCD $ 的边长为 1,$ E,F $ 两点分别在边 $ AD,BC $ 上,将正方形 $ ABCD $ 沿着 $ EF $ 翻折,点 $ B $ 恰好落在边 $ CD $ 上的点 $ B' $ 处.若四边形 $ ABFE $ 与四边形 $ EFCD $ 的面积比为 $ 3:5 $,则 $ FC $ 的长为
$\frac{3}{8}$
.
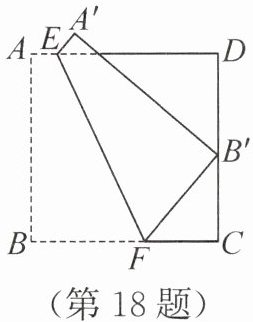
答案:18. $\frac{3}{8}$ 解析:如图,连接$BB'$交$EF$于点$G$,过点$F$作$FH⊥ AD$于点$H$,则$\angle FHD=\angle FHE = 90^{\circ}$。因为四边形$ABCD$是边长为$1$的正方形,四边形$ABFE$与四边形$EFCD$的面积比为$3:5$,所以$S_{\mathrm{四边形}ABFE}=\frac{3}{3 + 5}×1×1=\frac{3}{8}$,$\angle C=\angle D = 90^{\circ}$,$AB = AD = CD = BC = 1$,$AD// BC$。所以$\angle BFH=\angle FHD = 90^{\circ}$,四边形$CDHF$是矩形,即$DH = CF$,$FH = CD$。所以$FH = BC$。设$CF = x$,则$DH = x$,$BF = 1 - x$。所以$S_{\mathrm{四边形}ABFE}=\frac{1}{2}(AE + BF)· AB=\frac{3}{8}$,即$\frac{1}{2}(AE + 1 - x)×1=\frac{3}{8}$,解得$AE = x-\frac{1}{4}$。所以$DE = AD - AE = \frac{5}{4}-x$。所以$EH = DE - DH=\frac{5}{4}-2x$。由翻折的性质,得$B'F = BF = 1 - x$,$BB'⊥ EF$,即$\angle BGF = 90^{\circ}$。所以$\angle1+\angle2 = 90^{\circ}$。因为$\angle2+\angle3 = 90^{\circ}$,所以$\angle1=\angle3$。又$\angle FHE=\angle C = 90^{\circ}$,所以$\triangle EFH\cong\triangle B'BC(ASA)$。所以$EH = B'C$,即$B'C=\frac{5}{4}-2x$。在$\mathrm{Rt}\triangle B'FC$中,由勾股定理,得$B'F^{2}=CF^{2}+B'C^{2}$,所以$(1 - x)^{2}=x^{2}+(\frac{5}{4}-2x)^{2}$,即$4x^{2}-3x+\frac{9}{16}=0$。所以$(2x-\frac{3}{4})^{2}=0$。所以$2x-\frac{3}{4}=0$,即$x=\frac{3}{8}$。所以$FC$的长为$\frac{3}{8}$。
