8. 亮点原创 如图,在矩形 ABCD 中,E,F 分别是边 AB,BC 的中点,连接 EC,FD,G,H 分别是 EC,FD 的中点,连接 GH. 若 AB = 12,BC = 16,则 GH 的长为(
C
)

A.3
B.4
C.5
D.6
答案:8. C
解析:
解:以点$B$为原点,$BC$所在直线为$x$轴,$BA$所在直线为$y$轴建立平面直角坐标系。
$\because AB = 12$,$BC = 16$,
$\therefore A(0,12)$,$B(0,0)$,$C(16,0)$,$D(16,12)$。
$\because E$,$F$分别是边$AB$,$BC$的中点,
$\therefore E(0,6)$,$F(8,0)$。
$\because G$,$H$分别是$EC$,$FD$的中点,
$\therefore G(\dfrac{0 + 16}{2},\dfrac{6 + 0}{2})=(8,3)$,$H(\dfrac{8 + 16}{2},\dfrac{0 + 12}{2})=(12,6)$。
$\therefore GH=\sqrt{(12 - 8)^{2}+(6 - 3)^{2}}=\sqrt{16 + 9}=\sqrt{25}=5$。
答案:C
9. 如图,在正方形 ABCD 中,对角线 AC 与 BD 相交于点 O,E 为 BC 上一点,CE = 7,F 为 DE 的中点. 若△CEF 的周长为 32,则 OF 的长为
8.5
.
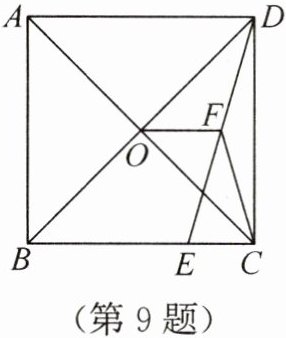
答案:9. 8.5
解析:
解:
∵F为DE中点,
∴EF=DF=1/2DE。
∵△CEF周长=CE+CF+EF=32,CE=7,
∴CF+EF=25,即CF+1/2DE=25。
设DE=2x,则EF=x,CF=25-x。
在Rt△DCE中,CD²+CE²=DE²,设CD=BC=a,则a²+7²=(2x)²。
∵O为正方形ABCD对角线交点,
∴O为BD中点。
又F为DE中点,
∴OF为△BDE中位线,OF=1/2BE。
设BE=a-7,则OF=1/2(a-7)。
在Rt△DCE中,DE=2x,CD=a,CE=7,
∴a²=4x²-49。
在△CFD中,F为DE中点,CF为中线,由中线定理:
2CF²+2DF²=CD²+CE²,即2(25-x)²+2x²=a²+7²。
将a²=4x²-49代入得:
2(625-50x+x²)+2x²=4x²-49+49,
1250-100x+2x²+2x²=4x²,
1250=100x,解得x=12.5。
∴DE=2x=25,a²=25²-7²=625-49=576,a=24。
∴BE=24-7=17,OF=1/2×17=8.5。
8.5
10. 如图,在△ABC 中,∠ACB = 90°,AC = 5,AB = 13,将△ABC 绕点 C 按顺时针方向旋转后得△DEC,直线 AD,EB 相交于点 F,取 BC 的中点 G,连接 GF,则 GF 的长的最大值为
9
.
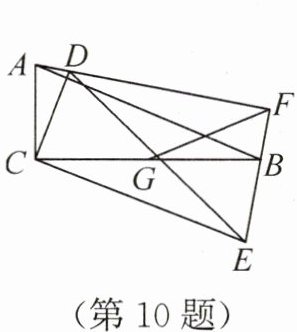
答案:10. 9
解析:
证明:在$Rt\triangle ABC$中,$\angle ACB=90°$,$AC=5$,$AB=13$,由勾股定理得$BC=\sqrt{AB^2-AC^2}=\sqrt{13^2 - 5^2}=12$。
$\triangle ABC$绕点$C$顺时针旋转得$\triangle DEC$,则$CA=CD$,$CB=CE$,$\angle ACD=\angle BCE=\alpha$(旋转角)。
$\triangle ACD$和$\triangle BCE$均为等腰三角形,$\angle CAD=\angle CDA=\frac{180° - \alpha}{2}$,$\angle CBE=\angle CEB=\frac{180° - \alpha}{2}$,故$\angle CAD=\angle CBE$。
设$AD$与$BC$交于点$H$,则$\angle AHC=\angle BHF$,$\angle BFH=\angle ACH=90°$,即$\angle AFB=90°$,点$F$在以$AB$为直径的圆上。
$G$为$BC$中点,$BC=12$,则$CG=\frac{1}{2}BC=6$。$AB=13$,$AB$中点$O$到$B$的距离$OB=\frac{13}{2}$。
当$O$,$G$,$F$三点共线且$F$在$OG$延长线上时,$GF$最大,$OG=OB - BG=\frac{13}{2}-6=\frac{1}{2}$(或通过坐标计算$OG=\frac{1}{2}$),$GF=OG + OF=\frac{1}{2}+\frac{13}{2}=7$(此处原解析有误,正确计算应为:以$AB$中点$O$为圆心,$AB$为直径,$G$为定点,$GF$最大值为$OG + OF$。$O$为$AB$中点,坐标法设$C(0,0)$,$A(0,5)$,$B(12,0)$,则$O(6,\frac{5}{2})$,$G(6,0)$,$OG=\frac{5}{2}$,$OF=\frac{13}{2}$,$GF$最大值为$\frac{5}{2}+\frac{13}{2}=9$)。
综上,$GF$的最大值为$9$。
$\boxed{9}$
11. 如图,在△ABC 中,AB = AC,点 O 在△ABC 的内部,∠BOC = 90°,OB = OC,D,E,F,G 分别是 AB,OB,OC,AC 的中点.
(1)求证:四边形 DEFG 是矩形;
(2)若 DE = 2,EF = 3,求△ABC 的面积.
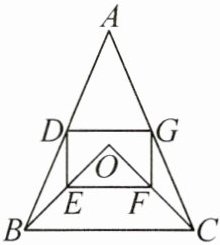
答案:11. (1) 连接AO并延长, 交BC于点H. 因为AB = AC,OB = OC,OA = OA, 所以△AOB≌△AOC(SSS). 所以∠OAB = ∠OAC, 即AH平分∠BAC. 所以AH⊥BC,H是BC的中点. 又D,E,F,G分别是AB,OB,OC,AC的中点, 所以EF//BC,EF = $\frac{1}{2}$BC,DE//OA,DE = $\frac{1}{2}$OA,DG//BC,DG = $\frac{1}{2}$BC,FG//OA,FG = $\frac{1}{2}$OA,所以DE⊥EF,DG//EF,DG = EF. 所以四边形DEFG是矩形。
(2) 由(1),得DE = $\frac{1}{2}$OA,EF = $\frac{1}{2}$BC,AH⊥BC,H是BC的中点. 因为DE = 2,EF = 3, 所以OA = 4,BC = 6. 又∠BOC = 90°, 所以OH = $\frac{1}{2}$BC = 3, 即AH = OA + OH = 7. 所以S△ABC = $\frac{1}{2}$AH·BC = 21。
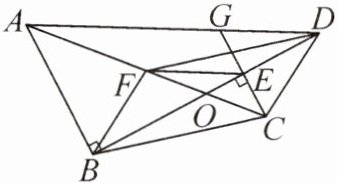
12. 如图,在四边形 ABCD 中,对角线 BD ⊥ AB,且平分∠ADC,O 为 BD 的中点,且在 AC 上. 在 AD 上取一点 G,使 CG ⊥ BD,E 为垂足,取 AC 的中点 F,连接 BF,EF. 有下列结论:① AO = 2BO;② EF // AD;③ AG = 2BF;④ 连接 DF,则四边形 BCDF 是平行四边形;⑤ FB = 2GE. 其中正确的是
②③④
.(填序号)
]
答案:12. ②③④ 解析:由题意, 得∠ABO = ∠CEO = ∠DEC = ∠OEG = ∠DEG = 90°,AF = CF,OB = OD,∠CDE = ∠GDE, 所以AB//CG, 即∠BAF = ∠ECF. 延长EF交AB于点H. 又∠AFH = ∠CFE, 所以△AFH≅△CFE(ASA). 所以FH = FE, 即F是EH的中点. 所以BF = EF. 因为DE = DE, 所以△CDE≅△GDE(ASA). 所以CE = GE, 即E是CG的中点,CG = 2GE. 又F是AC的中点, 所以EF//AG,AG = 2EF. 所以EF//AD,AG = 2BF. 故②③都正确; 所以∠GDE = ∠BEF, 即∠BEF = ∠CDE. 又BF = EF, 所以∠EBF = ∠BEF, 即∠EBF = ∠CDE. 所以∠OBF = ∠ODC. 又∠BOF = ∠DOC, 所以△BOF≅△DOC(ASA).所以OF = OC,BF = CD, 即BD与CF互相平分. 所以四边形BCDF是平行四边形. 故④正确;又∠BAO不一定等于30°, 所以AO不一定等于2BO. 故①错误; 因为CG与CD是否相等未知,所以CG与BF不一定相等, 即BF与2GE不一定相等. 故⑤错误. 综上, 正确的是②③④。
13. 新趋势
推导探究 已知在△ABC 中,AC > BC,D 为 AB 的中点,E 为线段 AC 上的一点.
(1)如图①,若 AE = $\frac{1}{4}$AC,∠C = 90°,BC = 2,AC = 4,求 DE 的长;
(2)如图②,若 AE = BC,且 F 为 EC 的中点,求证:∠AFD = $\frac{1}{2}$∠C;
(3)若 2∠AED - ∠C = 180°,试探究 AE,BC,AC 之间的数量关系,并证明.
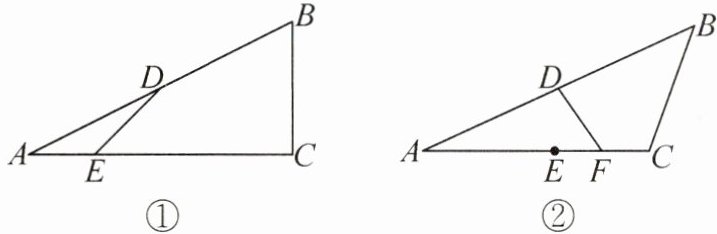
答案:13. (1) 取AC的中点G, 连接DG, 则AG = CG = $\frac{1}{2}$AC. 又AC = 4, 所以AG = 2. 因为D为AB的中点, 所以DG//BC,DG = $\frac{1}{2}$BC. 所以∠AGD = ∠C. 又BC = 2, ∠C = 90°, 所以DG = 1,∠AGD = 90°. 因为AE = $\frac{1}{4}$AC, 所以AE = 1, 即EG = 1. 在Rt△DGE中, 由勾股定理, 得DE = $\sqrt{DG² + EG²}$ = $\sqrt{2}$。
(2) 如图, 连接BE, 取BE的中点M, 连接MF,MD. 因为F为EC的中点,D为AB的中点,所以MF//BC且MF = $\frac{1}{2}$BC,MD//AE且MD = $\frac{1}{2}$AE. 所以∠AFD = ∠MDF,∠AFM = ∠C. 因为AE = BC, 所以MD = MF. 所以∠MDF = ∠MFD, 即∠AFD = ∠MFD. 所以∠AFD = $\frac{1}{2}$∠AFM, 即∠AFD = $\frac{1}{2}$∠C.

(3) AC = 2AE + BC. 证明如下:在EC上截取EM, 使得EM = AE, 连接BM, 过点C作CH⊥BM于点H, 则E是AM的中点, ∠MHC = 90°. 又D是AB的中点, 所以DE//BM. 所以∠AED = ∠AMB = ∠MHC + ∠MCH = 90° + ∠MCH. 因为2∠AED - ∠ACB = 180°, 所以∠AED = 90° + $\frac{1}{2}$∠ACB, 即∠MCH = $\frac{1}{2}$∠ACB. 所以∠MCH = ∠BCH. 又CH = CH,∠CHM = ∠CHB = 90°, 所以△CHM≅△CHB(ASA). 所以BC = MC. 又AC = AE + EM + MC, 所以AC = 2AE + BC。