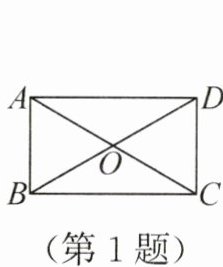
1. (教材 P74 练习 1 变式)(2024·甘肃白银)如图,在矩形 ABCD 中,对角线 AC,BD 相交于点 O,∠ABD = 60°,AB = 2,则 AC 的长为(
C
)
A.6
B.5
C.4
D.3
答案:1.C
解析:
证明:
∵四边形$ABCD$是矩形,
∴$AC = BD$,$OA=\frac{1}{2}AC$,$OB=\frac{1}{2}BD$,$\angle BAD = 90°$,
∴$OA = OB$,
∵$\angle ABD=60°$,
∴$\triangle AOB$是等边三角形,
∴$OA = AB = 2$,
∴$AC=2OA = 4$。
C
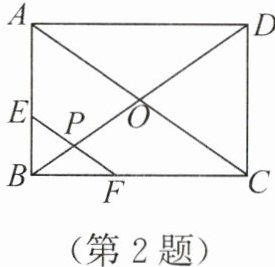
2. (2025·甘肃兰州)如图,四边形 ABCD 是矩形,对角线 AC,BD 相交于点 O,E,F 两点分别在边 AB,BC 上,连接 EF 交对角线 BD 于点 P. 若 P 为 EF 的中点,∠ADB = 35°,则∠DPE 的度数为(
C
)
A.95°
B.100°
C.110°
D.145°
答案:2.C
解析:
证明:
∵四边形$ABCD$是矩形,
∴$\angle BAD = 90°$,$AD // BC$,$OB = OD$(矩形对角线相等且互相平分)。
∵$\angle ADB = 35°$,
∴$\angle DBC = \angle ADB = 35°$(两直线平行,内错角相等)。
∵$P$为$EF$的中点,
∴$PE = PF$(中点定义)。
在$\triangle BEF$中,$PE = PF$,
∴$\angle PBF = \angle PEB = 35°$(等边对等角)。
∵$\angle DPE$是$\triangle PEB$的外角,
∴$\angle DPE = \angle PEB + \angle PBE = 35° + 75° = 110°$(三角形外角等于不相邻两内角之和)。
答案:C
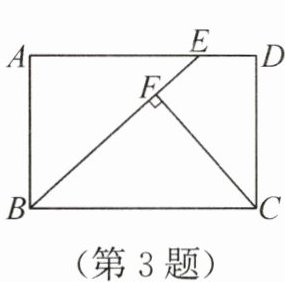
3. 如图,在矩形 ABCD 中,AB = 2,AD = 3,在边 AD 上取一点 E,连接 BE,使 BE = BC,过点 C 作 CF⊥BE,垂足为 F,则 BF 的长为
$\sqrt{5}$
.
答案:3.$\sqrt{5}$
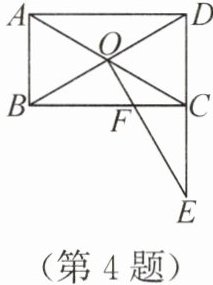
4. 亮点原创·如图,矩形 ABCD 的对角线 AC,BD 相交于点 O,AB = $\sqrt{3}$,∠ACB = 30°,延长 DC 至点 E,使得 CE = DC,连接 OE 交 BC 于点 F,则 CF 的长为
1
.
答案:4.1
解析:
解:在矩形$ABCD$中,$AB = CD=\sqrt{3}$,$\angle ABC = 90^{\circ}$,$O$为$AC$中点。
在$\mathrm{Rt}\triangle ABC$中,$\angle ACB = 30^{\circ}$,$\tan\angle ACB=\frac{AB}{BC}$,即$\tan30^{\circ}=\frac{\sqrt{3}}{BC}$,$\frac{\sqrt{3}}{3}=\frac{\sqrt{3}}{BC}$,解得$BC = 3$。
$CE=DC=\sqrt{3}$,则$DE=DC + CE=2\sqrt{3}$。
设$CF=x$,则$BF=BC - CF=3 - x$。
因为$AB// DE$,所以$\triangle OFB∼\triangle OED$。
$\frac{BF}{DE}=\frac{OB}{OD}$,又$OB = OD$,故$\frac{3 - x}{2\sqrt{3}}=\frac{1}{2}$,解得$x = 1$。
$\therefore CF=1$。
5. (2024·陕西 A 卷)如图,四边形 ABCD 是矩形,点 E 和点 F 在边 BC 上,且 BE = CF,连接 AF,DE. 求证:AF = DE.

答案:5.因为四边形ABCD是矩形,所以AB=DC,∠B=∠C=90°.又BE=CF,所以BE+EF=CF+EF,即BF=CE.所以△ABF≌△DCE(SAS).所以AF=DE.
解析:
证明:
∵四边形$ABCD$是矩形,
∴$AB = DC$,$\angle B=\angle C = 90°$。
∵$BE=CF$,
∴$BE + EF=CF + EF$,即$BF=CE$。
在$\triangle ABF$和$\triangle DCE$中,
$\begin{cases}AB=DC\\\angle B=\angle C\\BF=CE\end{cases}$,
∴$\triangle ABF\cong\triangle DCE(\mathrm{SAS})$。
∴$AF = DE$。
6. 如图,在矩形 ABCD 中,E 为 BA 延长线上一点,连接 CE,F 为 CE 的中点,以点 B 为圆心,BF 的长为半径的圆弧过 AD 与 CE 的交点 G,连接 BG. 若 AB = 4,CE = 10,则 AG 的长为(
C
)
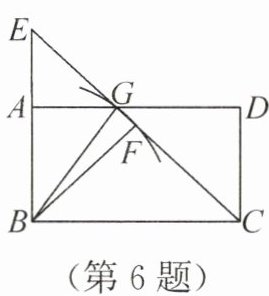
A.2
B.2.5
C.3
D.3.5
答案:6.C
解析:
解:
∵四边形$ABCD$是矩形,$AB=4$,
∴$AB=CD=4$,$AD// BC$,$\angle EBC=90°$。
∵$F$为$CE$中点,$CE=10$,
∴$BF=\frac{1}{2}CE=5$(直角三角形斜边中线等于斜边一半)。
∵$BG=BF$(同圆半径),
∴$BG=5$。
设$AG=x$,则$DG=AD - x$,$AE=y$,$BE=AB + AE=4 + y$。
在$Rt\triangle EBC$中,$BC^2 + BE^2=CE^2$,即$BC^2 + (4 + y)^2=10^2$①。
∵$AD// BC$,
∴$\triangle EAG∼\triangle EBC$,
∴$\frac{AG}{BC}=\frac{AE}{BE}$,即$\frac{x}{BC}=\frac{y}{4 + y}$②。
在$Rt\triangle ABG$中,$AG^2 + AB^2=BG^2$,即$x^2 + 4^2=5^2$,
解得$x=3$($x=-3$舍去)。
∴$AG=3$。
答案:C
7. 如图,在矩形 ABCD 中,AB = 1,∠CBD = 14°,将矩形 ABCD 绕对角线 BD 的中点 O 按逆时针方向旋转角度 α(0° < α < 90°)得到矩形 A'B'C'D',当 C',D 两点的距离等于 1 时,α 等于(
D
)
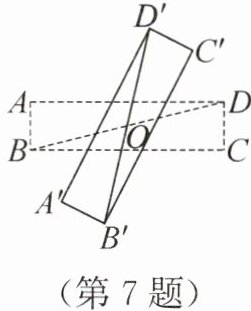
A.28°
B.42°
C.48°
D.56°
答案:7.D