1. 32 的因数有(
6
)个,从中选择四个因数,把它们组成一个比例,使两个比的比值等于$\frac{1}{2}$,这个比例是(
1:2=4:8(答案不唯一)
)。
答案:1. 6 1:2=4:8(答案不唯一)
2. 写出比值都是 0.8 的两个比,组成比例,使比例的两个外项分别是 1.6 和 4,这个比例是(
1.6:2=3.2:4
)或(
4:5=1.28:1.6
)。
答案:2. 1.6:2=3.2:4 4:5=1.28:1.6
3. 将底是 4 厘米,高是 3 厘米的平行四边形按(
3:1
)的比放大,可得底是 12 厘米,高是(
9
)厘米的平行四边形,新平行四边形和原图形的面积比是(
9:1
)。
答案:3. 3:1 9 9:1
4. 已知$\frac{m}{15} = \frac{n}{4}$($m$、$n$均不为 0),那么$m:n =$(
15
)$:$(
4
)。
答案:4. 15 4
5. 在比例尺为$1:400000$的地图上,量得常州到南京的图上距离为 34 厘米。一辆货车在 10 时 15 分以每小时 68 千米的速度从常州出发,预计(
12
)时(
15
)分到达南京。
答案:5. 12 15
解析:
实际距离 = 图上距离 ÷ 比例尺 = 34 ÷ (1/400000) = 34 × 400000 = 13600000 厘米 = 136 千米
时间 = 路程 ÷ 速度 = 136 ÷ 68 = 2 小时
10 时 15 分 + 2 小时 = 12 时 15 分
12 15
6. 一幅地图的比例尺如图:
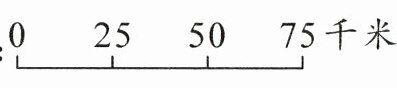
。在这幅地图上,图上距离和实际距离的比是(
1:2500000
);从周庄古镇到南京的实际距离是 270 千米,在这幅地图上两地的距离是(
10.8
)厘米。
答案:6. 1:2500000 10.8
7. 用 4,3,15 和$x$组成比例,$x$最小是(
0.8
),这个比例是(
4:15=0.8:3(答案不唯一)
);$x$最大是(
20
),这个比例是(
4:20=3:15(答案不唯一)
)。
答案:7. 0.8 4:15=0.8:3(答案不唯一) 20 4:20=3:15(答案不唯一)
8. 一个半径是 4 厘米的圆,按$2:1$的比放大后,圆的面积是(
200.96
)平方厘米;按(
1:4
)的比缩小后,圆的面积是 3.14 平方厘米。
答案:8. 200.96 1:4
9. 如图,4 个相同的直角三角形拼成了一个正方形,已知$a:b = 1:2$,则涂色部分的面积占大正方形面积的$\frac{(\ \ \ \ \ )}{(\ \ \ \ \ )}$。
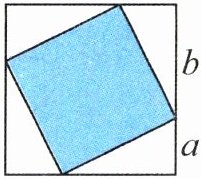
答案:9. $\frac{5}{9}$
解析:
设$a = k$,则$b = 2k$。
直角三角形面积:$\frac{1}{2}ab=\frac{1}{2}× k× 2k=k^{2}$,4个三角形面积:$4k^{2}$。
大正方形边长:$a + b=3k$,面积:$(3k)^{2}=9k^{2}$。
涂色部分面积:$9k^{2}-4k^{2}=5k^{2}$。
占比:$\frac{5k^{2}}{9k^{2}}=\frac{5}{9}$。
$\frac{5}{9}$
10. 小华和小明分别从一座桥的两端同时出发,往返于桥的两端之间。小华的速度是 60 米/分,小明的速度是 65 米/分,经过 12 分钟两人第二次相遇。这座桥长(
500
)米。在一幅地图上,量得这座桥的图上距离是 2.5 厘米,这幅地图的比例尺是(
1:20000
)。
答案:10. 500 1:20000 解析:小华和小明从桥的两端同时出发到第二次相遇,一共走了3个全程,桥长为(60+65)×12÷3=500(米)。
解析:
(60+65)×12÷3=500(米)
500米=50000厘米
2.5:50000=1:20000
11. 如图,两个正方形中涂色部分的面积比是$2:1$,如果空白部分甲的面积是 2.4 平方分米,那么两个正方形的面积之和是(
4
)平方分米。
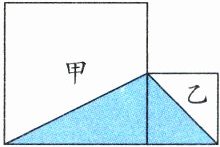
答案:11. 4 解析:已知涂色部分两个小三角形的面积比是2:1,高都是小正方形的边长,高相同,则涂色部分两个小三角形的底之比是2:1,也就是两个正方形的边长之比是2:1,则大正方形与小正方形的面积比是4:1。将小正方形的面积看作1份,则大正方形的面积是这样的4份,观察题图可知甲的面积是这样的3份,即可求出1份的面积为2.4÷(4−1)=0.8(平方分米),也就是小正方形的面积,进而可以求出两个正方形的面积之和,即0.8×4+0.8=4(平方分米)。
解析:
因为涂色部分两个三角形面积比是$2:1$,且高相同(均为小正方形边长),所以底之比为$2:1$,即大、小正方形边长比为$2:1$,面积比为$4:1$。
设小正方形面积为$x$平方分米,则大正方形面积为$4x$平方分米。
空白部分甲的面积为大正方形面积减去大三角形面积,大三角形底为大正方形边长,高为小正方形边长,面积为$\frac{1}{2}×2a× a = a^2$(设小正方形边长为$a$,则大正方形边长为$2a$,小正方形面积$x = a^2$),所以甲的面积为$4x - x = 3x$。
已知甲的面积是$2.4$平方分米,可得$3x = 2.4$,解得$x = 0.8$。
两个正方形面积之和为$4x + x = 5x = 5×0.8 = 4$平方分米。
4