6. 函数 $ y = 4x^2 - 1 $ 的图像与 $ y $ 轴的交点坐标是
,与 $ x $ 轴的交点坐标是
。
答案:(0,-1)
$(\frac 12,$0),$(-\frac 12,$0)
7. 若函数 $ y = ax^2 - 3 $ 的图像可以由函数 $ y = -x^2 $ 的图像平移得到,则 $ a $ 的值是
-1
。
答案:-1
8. 把函数 $ y = -2x^2 $ 的图像向左平移 $ 2 $ 个单位长度,所得图像的函数表达式为(
C
)。
A.$ y = -2x^2 + 2 $
B.$ y = -2x^2 - 2 $
C.$ y = -2(x + 2)^2 $
D.$ y = -2(x - 2)^2 $
答案:C
9. 对于函数 $ y = -(x + 2)^2 $,下列叙述中,正确的是(
D
)。
A.图像的顶点坐标是 $ (2, 0) $
B.当 $ x < 0 $ 时,$ y $ 随 $ x $ 的增大而增大
C.当 $ x = 0 $ 时,$ y $ 有最大值
D.当 $ x > -2 $ 时,$ y $ 随 $ x $ 的增大而减小
答案:D
10. 试说明函数 $ y = 3(x - 2)^2 $ 的图像可以由函数 $ y = 3x^2 - 1 $ 的图像经过怎样的平移得到。
答案:解:由函数$y=3x^2-1$的图像先向上平移1个单位长度,再向右平移2个单位长度得到
或由函数$y=3x^2-1$的图像先向右平移2个单位长度,再向上平移1个单位长度得到
11. 已知二次函数 $ y = -2(x + a)^2 + (1 - a) $ 的图像的顶点在坐标轴上。求 $ a $ 的值。
答案:解:当顶点在x轴上时,1-a=0,∴a的值为1;
当顶点在y轴上时,a的值为0
12. 函数可揭示事物变化的规律,它有多种表示形式,如表格、图像、表达式等,这些表示形式各有优势:图像法直观,列表法具体,表达式精确。若把三者结合起来,则能更全面深刻地理解变量之间的关系。试解决下列问题:
(1)已知函数表达式 $ y = \frac{2}{x^2} $,你能说出它的图像具有的一些特征吗?试画出它的图像。
(2)试说明下列函数的图像与函数 $ y = \frac{2}{x^2} $ 的图像之间的位置关系,并在同一平面直角坐标系中画出它们的图像。
① $ y = \frac{2}{x^2} - 2 $;
② $ y = \frac{2}{(x - 1)^2} $。
答案:解:(1)∵x、y都不能等于0
∴图像与坐标轴无交点
∵x的值取正数或负数时,y的值都是正数
∴图像位于第二象限
∵当$x\gt 0$时,y随x的增大而减小
∴在第一象限的图像从左往右看是下降的
同样,在第二象限的图像从左往右看是上升的
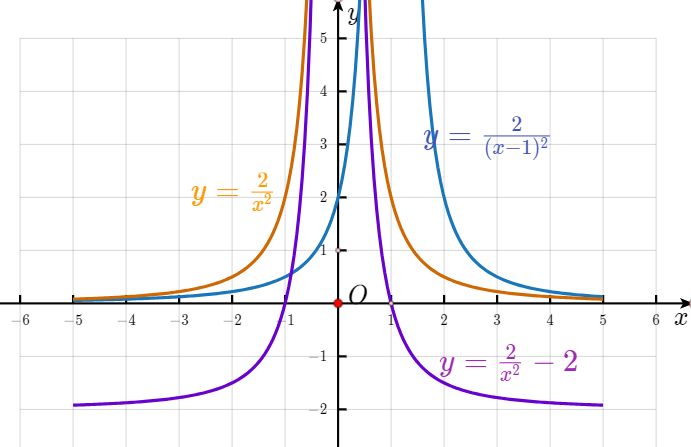
(2)①函数$y=\frac {2}{x^2} -2$的图像可以由函数$y=\frac {2}{x^2} $的图像向下平移2个单位长度得到
②函数$y=\frac {2}{(x-1)^2} $的图像可以由函数$=\frac {2}{x^2} $的图像向右平移1个单位长度得到