1. 函数 $ y = \frac{1}{2}x^2 - 3 $ 的图像开口向
上
,顶点坐标为
(0,-3)
,对称轴是
y轴
,其图像可以由函数 $ y = \frac{1}{2}x^2 $ 的图像沿 $ y $ 轴向
下
平移
3
个单位长度得到。
答案:上
(0,-3)
y轴
下
3
2. 函数 $ y = -2(x - 3)^2 $ 的图像开口向
下
,顶点坐标为
(3,0)
,对称轴是过点
(3,0)
且与 $ y $ 轴平行的直线,其图像可以由函数 $ y = -2x^2 $ 的图像沿 $ x $ 轴向
右
平移
3
个单位长度得到。
答案:下
(3,0)
(3,0)
右
3
3. 当 $ x = $
0
时,函数 $ y = \frac{1}{2}x^2 + 2 $ 取得最
小
值,最
小
值是
2
。
答案:0
小
小
2
4. 已知点 $ (a, 6) $ 在函数 $ y = \frac{1}{2}x^2 + 4 $ 的图像上,则 $ a $ 的值为(
A
)。
A.$ -2 $ 或 $ 2 $
B.$ 2\sqrt{2} $ 或 $ -2\sqrt{2} $
C.$ 2 $
D.$ -2 $
答案:A
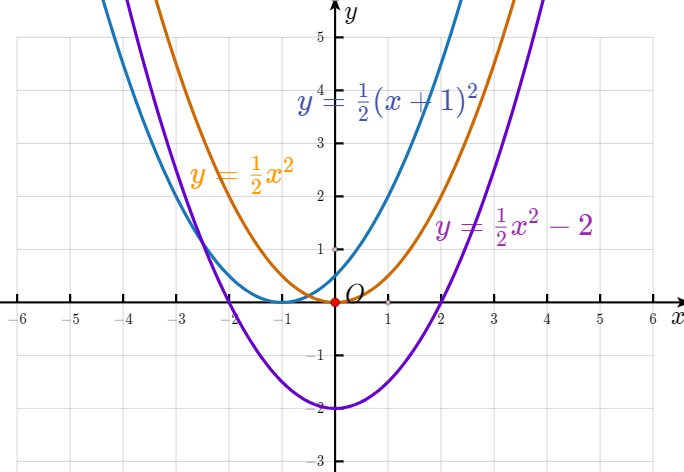
5. 分别说明下列函数的图像与函数 $ y = \frac{1}{2}x^2 $ 的图像之间的位置关系,并在同一平面直角坐标系中画出这 $ 3 $ 个函数的图像:
(1)$ y = \frac{1}{2}x^2 - 2 $;
(2)$ y = \frac{1}{2}(x + 1)^2 $。
答案:解:(1)函数$y=\frac 12x^2-2$可以由函数$y=\frac 12x^2$的图像沿y轴向下平移2个单位长度得到
(2)函数$y=\frac 12(x+1)^2$可以由函数$y=\frac 12x^2$的图像沿x轴向左平移1个单位长度得到
如图所示