1. 填空:
- (1) $ x^{2} + 2x + $_________$ = (x + $_________$)^{2} $;
- (2) $ x^{2} - \frac{3}{2}x + $_________$ = (x - $_________$)^{2} $.
答案:1
1
$ \frac{9}{16}$
$ \frac{3}{4}$
2. 函数 $ y = -\frac{3}{4}x^{2} $ 的图像沿 $ x $ 轴向左平移 $ 2 $ 个单位长度,再沿 $ y $ 轴向上平移 $ 3 $ 个单位长度,可得到函数
$ y = - \frac{3}{4}(x + 2)^2 + 3 $
的图像.
答案:$y=-\frac {3}{4}(x+2)^2+3$
3. 函数 $ y = -(x + 1)^{2} + 3 $ 的图像开口向
下
,顶点坐标是
$ (-1,3) $
,对称轴是
过点$(-1,3)$且平行于$y$轴的直线
.
答案:下
(-1,3)
过点(-1,3)且平行于y轴的直线
4. 用配方法求下列函数的顶点坐标和对称轴:
- (1) $ y = x^{2} + 4x + 1 $;
- (2) $ y = -2x^{2} + 2x - 1 $.
答案:解:$(1)y=x^2+4x+4-3=(x+2)^2-3$
顶点坐标是(-2,-3), 对称轴是过点(-2,-3)且平行于y轴的直线
$(2)y=-2(x^2-x)-1=-2(x-\frac 12)^2-\frac 12$
顶点坐标是$(\frac {1}{2} ,$$-\frac {1}{2} ) ,$对称轴是过点$(\frac {1}{2},$$- \frac {1}{2} )$且平行于y轴的直线
5. 已知函数 $ y = -\frac{1}{2}(x - 2)^{2} + 1 $.
- (1) 画出这个函数的图像.
- (2) $ x $ 在什么范围内取值时,$ y $ 随 $ x $ 的增大而增大?
- (3) 这个函数的图像可以由函数 $ y = -\frac{1}{2}x^{2} $ 的图像怎样平移得到?
答案:解:(1)如图所示
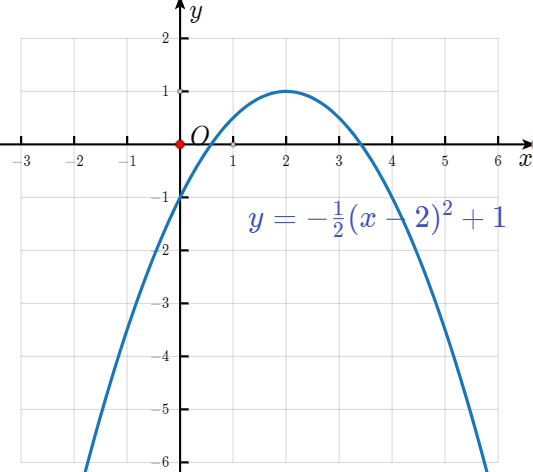
(2)由图可知,当x<2时,y随x的增大而增大
(3)函数$y=- \frac {1}{2} (x-2)^2+1$的图像可以由函数$y=\frac {1}{2} x^2$的图像
先沿x轴向右平移2个单位长度,再沿y轴向上平移1个单位长度得到