17. 如图,在$Rt\triangle ABC$中,$\angle B = 90^{\circ}$,$AB = 8$,$\angle CAB$的平分线$AD$交$BC$于点$D$,且$AD = \frac{16\sqrt{3}}{3}$. 求$\angle C$的度数及边$BC$、$AC$的长度(保留根号).

答案:解:在Rt△ABD中,∵AB=8,$AD=\frac {16\sqrt 3}3$
∴$cos∠DAB=\frac {AB}{AD}=\frac 8{\frac {16\sqrt 3}3}=\frac {\sqrt 3}2$
∴∠DAB=30°
∴AD平分∠CAB
∴∠CAB=2∠DAB=60°
∴∠C=30°
在Rt△ABC中,∵AB=8,∠C=30°
∴$BC=\sqrt 3AB=8\sqrt 3,$AC=2AB=16
18. 在$\triangle ABC$中,$\angle B = 45^{\circ}$,$\cos A = 0.8$.
(1) 试通过查找下表,推断出$\triangle ABC$的形状;

(2) $\triangle ABC$的边$AC$上的高$BD = 3$,求$BC$的长.
答案:解:(1)∵cos 36°50'=0.8004,cos 37°=0.7986,cos A=0.8
∴$36°50'\lt ∠A\lt 37°,$$98°\lt ∠ C\lt 98°10'$
∴△ABC是钝角三角形
(2) 如图,BD是边AC上的高,BD⊥AC,BD=3,过点C作CE⊥AB,垂足为E
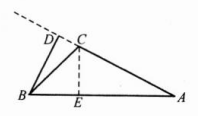
在Rt △ABD中,$cos A=\frac {AD}{AB}=\frac {4}{5}$
设AD=4k,AB=5k
∴$3^2+(4k)^2=(5k)^2,$k=1
∴AB=5,AD=4
在Rt△ACE中,$cosA=\frac {AE}{AC}=\frac {4}{5}$
设AE=4a,AC=5a
∴$CE=\sqrt{(5a)^2-(4a)^2}=3a$
又∵∠CBE=45°,∠BEC=90°
∴BE=CE=3a
∵BE+AE=AB
∴3a+4a=5
∴$a=\frac {5}{7}$
∴$BE=CE=\frac {15}{7}$
∴$BC=\frac {BE}{cos_{45}°}=\frac {15}{7} × \frac {2}{\sqrt 2}=\frac {15\sqrt{2}}{7}$