10. 在$\triangle ABC$中,$AD$是边$BC$上的高,$AD = 2$,$AC = 2\sqrt{2}$,$AB = 4$. 求$\angle BAC$的度数.
(提示:应考虑$AD$在$\triangle ABC$内部和外部两种情况)
答案:解:分两种情况
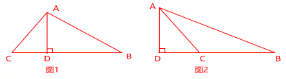
①AD在△ABC内部
在Rt△ACD中,∵AD=2,$AC=2\sqrt 2$
∴$cos∠CAD=\frac {AD}{AC}=\frac {\sqrt 2}2$
∴∠CAD=45°
在Rt△ABD中,∵AD=2,AB=4
∴$cos∠BAD=\frac {AD}{AB}=\frac 12$
∴∠BAD=60°
∴∠BAC=∠BAD+∠CAD=105°
②AD在△ABC外部
同理∠BAD=60°,∠CAD=45°
∴∠BAC=∠BAD-∠CAD=15°
∴∠BAC的度数是105°或15°
11. 在$\triangle ABC$中,$\angle C = 90^{\circ}$. 若$BC = 4$,$AC = 4\sqrt{3}$,则$\angle A =$
30°
,$\angle B =$
60°
.
答案:30°
60°
12. 在$\triangle ABC$中,$\angle C = 90^{\circ}$. 若$\tan A = \sqrt{3}$,$BC = 2\sqrt{3}$,则$AB =$
4
,$AC =$
2
.
答案:4
2
13. 若$\angle A$、$\angle B$为锐角,且$\sqrt{3}\tan A - 3 = 0$,$2\cos B = \sqrt{3}$,则$\triangle ABC$是(
C
).
A.腰与底不相等的等腰三角形
B.等边三角形
C.两直角边不相等的直角三角形
D.等腰直角三角形
答案:C
14. 如果$\angle A$为锐角,且$\cos A = \frac{1}{4}$,那么(
D
).
A.$0^{\circ} < \angle A < 30^{\circ}$
B.$30^{\circ} < \angle A < 45^{\circ}$
C.$45^{\circ} < \angle A < 60^{\circ}$
D.$60^{\circ} < \angle A < 90^{\circ}$
答案:D
15. 根据下列条件,求锐角$\theta$的大小:
(1) $\sin \theta = \frac{\sqrt{3}}{2}$;
(2) $\cos \theta = \frac{\sqrt{3}}{2}$;
(3) $\tan \theta = \sqrt{3}$;
(4) $\tan \theta = 0.8972$.
答案:解:(1)θ=60°;(2)θ=30°;(3)θ=60°;(4)θ=41.9°
16. 某飞机在离地面$2400m$的上空的点$A$处测得地面控制点$B$的俯角为$60^{\circ}$,求此时飞机与该地面控制点之间的距离.

答案:解:令飞机A的正下方且位于地面上的点为点D
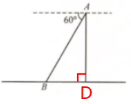
由题意得,AD⊥BD,$AD=2400\ \mathrm {m},$∠BAD=90°-60°=30°
在Rt△ABD中,∵∠BAD=30°,$AD=2400\ \mathrm {m}$
∴$AB=\frac {AD}{cos 30°}=1600\sqrt 3\ \mathrm {m}$
答:此时飞机与该地面控制点之间的距离为$1600\sqrt 3\ \mathrm {m}。$