13. 在$\triangle ABC$中,$\angle C = 90^{\circ}$,根据下列条件,求$\sin A$、$\cos A$:
(1) $AC = 2$,$BC = 3$;
(2) $3BC = \sqrt{3}AB$;
(3) $\tan B = \frac{3}{5}$.
答案:解:(1)在Rt△ABC中,∵AC=2,BC=3,∠C=90°
∴$AB=\sqrt {AC^2+BC^2}=\sqrt {13}$
∴$sinA=\frac {BC}{AB}=\frac 3{\sqrt {13}}=\frac {3\sqrt {13}}3,$$cosA=\frac {AC}{AB}=\frac 2{\sqrt {13}}=\frac {2\sqrt {13}}{13}$
(2)不妨设BC=1,则$AB=\sqrt 3$
在Rt△ABC中,∵BC=1,$AB=\sqrt 3,$∠C=90°
∴$AC=\sqrt {AB^2-BC^2}=\sqrt 2$
∴$sinA=\frac {BC}{AB}=\frac 1{\sqrt 3}=\frac {\sqrt 3}3,$$cos A=\frac {AC}{AB}=\frac {\sqrt 2}{\sqrt 3}=\frac {\sqrt 6}3$
$(3)tan B=\frac {AC}{BC}=\frac 35$
不妨设AC=3x,则BC=5x
在Rt△ABC中,∵AC=3x,BC=5x
∴$AB=\sqrt {AC^2+BC^2}=\sqrt {34}x$
∴$sinA=\frac {BC}{AB}=\frac {5x}{\sqrt {34}x}=\frac {5\sqrt {34}}{34},$$cosA=\frac {AC}{AB}=\frac {3x}{\sqrt {34}x}=\frac {3\sqrt {34}}{34}$
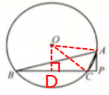
14. 如图,$\triangle ABC$是$\odot O$的内接三角形,点$P$在$BC$的延长线上,$PA$与$\odot O$相切,且$PA ⊥ PB$. 若$BC = 8$,$CP = 1$,求$\angle ABC$的正弦值.

答案:解:连接OA、OC,过点O作OD⊥BC,垂足为点D
∵PA与$\odot O$相切
∴OA⊥PA
∵OD⊥BC,PA⊥PB
∴四边形OAPD是矩形
∴OA=DP,OD=AP
∵BC=8,OD⊥BC
∴$CD=\frac 12BC=4$
∵CP=1
∴OA=DP=5
在Rt△OCD中,∵OC=OA=5,CD=4
∴$OD=\sqrt {OC^2-CD^2}=3$
∴AP=OD=3
在Rt△APB中,
∵AP=3,BP=BC+CP=9
∴$AB=\sqrt {AP^2+BP^2}=3\sqrt {10}$
∴$sin ∠ABC=\frac {AP}{AB}=\frac 3{3\sqrt {10}}=\frac {\sqrt {10}}{10}$
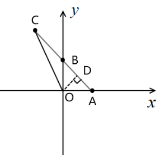
15. 在平面直角坐标系中,已知一条直线经过$A(2,0)$、$B(0,2)$、$C(-1,m)$,连接$OC$($O$为坐标原点). 求$\angle ACO$的正弦值.
答案:解:过点O作OD⊥AC,垂足为点D
设直线AC的函数表达式为y=kx+b
将点A(2,0)、B(0,2)代入得$\begin{cases}{2k+b=0}\\{b=2}\end{cases},$解得$\begin{cases}{k=-1}\\{b=2}\end{cases}$
∴直线AC的表达式为y=-x+2
将点C(-1,m)代入得m=3
∴点C的坐标为(-1,3)
∴$OC=\sqrt {(-1)^2+3^2}=\sqrt {10}$
∵OA=OB=2
∴∠OAB=45°
∵OD⊥AC
∴△OAD为等腰直角三角形
∴$OD=\frac {OA}{\sqrt 2}=\sqrt 2$
在Rt△OCD中,∵$OD=\sqrt 2,$$OC=\sqrt {10}$
∴$sin ∠ACO=\frac {OD}{OC}=\frac {\sqrt 2}{\sqrt {10}}=\frac {\sqrt 5}5$