5. 已知点 $ ( 1, a ) $ 在二次函数 $ y = - 3 x ^ { 2 } $ 的图像上,则 $ a $ 的值是
-3
. 此时,点 $ ( - 1, a ) $
在
(填“在”或“不在”)该图像上.
答案:-3
在
6. 已知点 $ ( - 3, y _ { 1 } ) $、$ ( - 2, y _ { 2 } ) $、$ ( - 1, y _ { 3 } ) $ 都在函数 $ y = x ^ { 2 } $ 的图像上,则(
C
).
A.$ y _ { 1 } < y _ { 2 } < y _ { 3 } $
B.$ y _ { 1 } < y _ { 3 } < y _ { 2 } $
C.$ y _ { 3 } < y _ { 2 } < y _ { 1 } $
D.$ y _ { 2 } < y _ { 1 } < y _ { 3 } $
答案:C
7. 在同一平面直角坐标系中,画出下列函数的图像:
(1) $ y = \frac { 3 } { 4 } x ^ { 2 } $;
(2) $ y = - \frac { 3 } { 4 } x ^ { 2 } $.
答案:解:如图所示

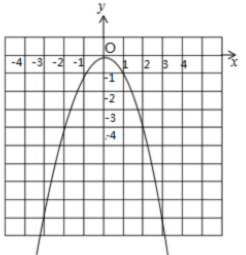
8. 画出二次函数 $ y = - x ^ { 2 } $ 的图像,并利用图像,求下列取值范围:
(1) 当 $ 2 < x < 3 $ 时,$ y $ 的取值范围;
(2) 当 $ - 2 < x < 3 $ 时,$ y $ 的取值范围;
(3) 当 $ - 4 < y < - 1 $ 时,$ x $ 的取值范围.
答案:解:函数图像如图所示
(1)由图可知,当2<x<3时,-9<y<-4
(2)当-2<x<3时,-9<y≤0
(3)由图可知,当-4<y<-1时,-2<x<-1或1<x<2
9. 已知长方体的高为 $ \frac { 1 } { 2 } \mathrm { cm } $,底面是边长为 $ x \mathrm { cm } $ 的正方形,该长方体的体积为 $ y \mathrm { cm } ^ { 3 } $.
(1) 写出 $ y ( \mathrm { cm } ^ { 3 } ) $ 与 $ x ( \mathrm { cm } ) $ 之间的函数表达式,指出自变量 $ x $ 的取值范围.
(2) 画出函数的图像.
(3) 根据图像,回答问题:① 当正方形的边长为 $ 3 \mathrm { cm } $ 时,求长方体的体积;② 当 $ x $ 满足什么条件时,$ y \geq 2 $?
答案:解:$(1)y=\frac 12×x · x=\frac 12x^2(x>0)$
(2)函数图像如下
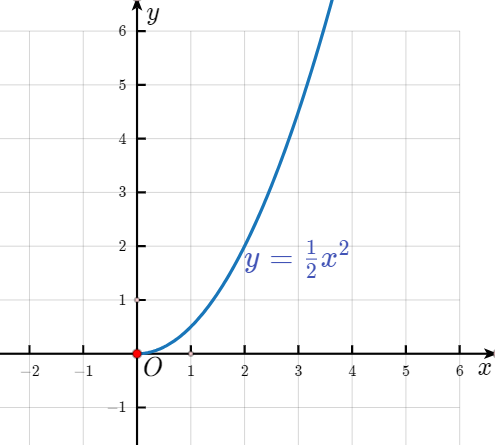
(3)①当$x=3\ \mathrm {cm} $时,$y=\frac 12×3^2=\frac 92\ \mathrm {cm^3}$
②若y≥2,即$\frac 12x^2≥2$
∴x≥2