6. 已知:如图,在$\triangle ABC$中,$DE // BC$,$EF // CD$。
(1) 写出图中的相似三角形,并选择一对加以证明;
(2) 若$AE = 5$,$EC = 3$,$EF = 4$,$BC = 7$,求$DE$、$CD$的长。

答案:解:(2)∵△ADE∽△ABC
∴$\frac {AE}{AC}=\frac {DE}{BC}$
∵AE=5,EC=3,BC=7
∴AC=AE+EC=8
∴$\frac 58=\frac {DE}7$
∴$DE=\frac {35}{8}$
∵EF//CD
∴△AFE∽△ADC
∴$\frac {AE}{AC}=\frac {EF}{CD},$即$\frac 58=\frac 4{CD}$
∴$CD=\frac {32}{5}$
7. 如图,$DE // FG // BC$,$DE = 2$,$FG = 3$,$BC = 5$,$AE = 4$,$DG$的延长线交$BC$延长线于点$H$。
(1) $EG =$
2
,$GC =$
4
;
(2) 求$CH$的长。

答案:(1)2 4
解:(2)
∵DE//FG//BC
∴△ADE∽△AFG
∴$\frac {DE}{FG}=\frac {AE}{AG}$
∵DE=2,FG=3,AE=4
∴$\frac 23=\frac 4{AG}$
∴AG=6,EG=2
同理可得,CG=4
∵EG=DE
∴∠EGD=∠EDG
∵DE//BC
∴∠EDG=∠H
∵∠EGD=∠CGH
∴∠CGH=∠H
∴CH=CG=4
8. 如图,$DE$是$\triangle ABC$的中位线,$F$是$DE$的中点,$CF$的延长线交$AB$于点$G$。求$AG:GD$。

答案:解:取CG 的中点H,连接EH
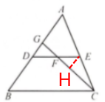
∵DE是△ABC的中位线
∴E是AC的中点
∵H是CG 的中点
∴EH是△ACG的中位线
∴EH//AG,AG=2HE
∴∠GDF=∠HEF
∵F 是DE的中点
∴DF=EF
在△DFG 和△EFH中
$\begin{cases}{∠GDF=∠HEF}\\{DF=EF}\\{∠GFD=∠HFE}\end{cases}$
∴$△DFG≌△EFH(\mathrm {ASA})$
∴GD=HE
∴AG:GD=2HE:HE=2:1
9. 如图,在$\triangle ABC$中,点$D$在$AC$上,点$E$在$BD$上,且$\frac{AD}{DC}=\frac{2}{3}$,$\frac{BE}{ED}=\frac{3}{2}$,$AE$的延长线交$BC$于点$F$。求$BF:FC$。

答案:解:作DG//AF{交}BC于点G
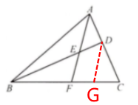
∵DG//AF
∴$\frac {AD}{CD}=\frac {FG}{CG},$$\frac {BE}{ED}=\frac {BF}{FG}$
∵$\frac {AD}{CD}=\frac 23,$$\frac {BE}{ED}=\frac 32$
∴$\frac {FG}{CG}=\frac 23,$$\frac {BF}{FG}=\frac 32$
设FG=2x,则CG=3x,BF=3x
∴FC=FG+CG=5x
∴BF:FC=3:5