6. 如图,$\triangle ADE \backsim \triangle ABC$,且 $AD:DB = 2:1$,则 $DE:BC$ 为(
C
).

A.$2:1$
B.$1:2$
C.$2:3$
D.$3:2$
答案:C
7. 观察下列图形,用线段将形状相同的图形连起来.

答案: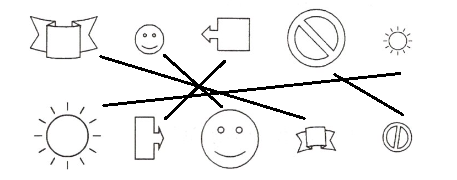
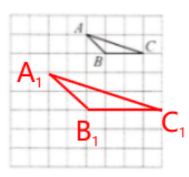
8. 如图,网格纸中画有格点三角形 $ABC$. 在图中画格点三角形 $A_1B_1C_1$,使 $\triangle A_1B_1C_1 \backsim \triangle ABC$,并写出它们的相似比.

答案:解:如图所示
相似比为2:1
9. 右面一组图形中的三角形都是相似三角形. 根据其规律,图⑩中共有
37
个三角形,其中最小的三角形与最大的三角形的相似比是
1:$2^{9}$
,面积比是
1:$2^{18}$
.

答案:37
1:$2^9$
1:$2^{18}$
10. 在长 $2\sqrt{2}$、宽 $1$ 的矩形纸片中,画两个小矩形,使这两个小矩形的每条边都与原矩形纸片的边平行,或小矩形的边在原矩形的边上,且每个小矩形均与原矩形纸片相似,然后将它们剪下,求所剪得的两个小矩形纸片周长之和的最大值.
答案:解:如图所示,剪下的两个小矩形纸片的周长之和最大
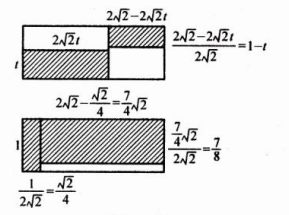
其中一个小矩形的长为1,则宽为$\frac 1{2\sqrt 2}=\frac {\sqrt 2}4$
另一个小矩形的长为$2\sqrt 2-\frac {\sqrt 2}4=\frac 74\sqrt 2$
$\frac {宽为\frac 74\sqrt 2}{2\sqrt 2}=\frac {7}{8}$
两小矩形的周长之和:$(1+\frac {\sqrt 2}4+\frac 74\sqrt 2+\frac {7}{8})=4\sqrt 2+\frac {15}{4}$
答:所剪得的两个小矩形纸片周长之和的最大值为$4\sqrt 2+\frac {15}{4}$