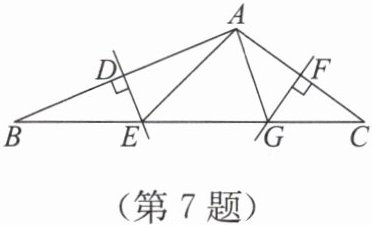
7. 如图，在△ABC中，∠BAC＞90°，AB的垂直平分线交BC于点E，交AB于点D，AC的垂直平分线交BC于点G，交AC于点F.当△AEG是等腰三角形时，∠B与∠C不可能有的数量关系是（ ）.
A. ∠B+2∠C=90°
B. ∠C+2∠B=90°
C. ∠B=∠C
D. 2∠C+$\frac{3}{2}$∠B=90°
答案：D
解析：AE=BE，AG=CG，∠B=∠BAE，∠C=∠CAG，∠EAG=∠BAC-∠B-∠C=180°-2∠B-2∠C.当AE=AG时，∠AEG=∠AGE，∠B+2∠C=90°；当AE=EG时，∠EAG=∠AGE，∠C+2∠B=90°；当AG=EG时，∠EAG=∠AEG，∠B=∠C.故D不可能.
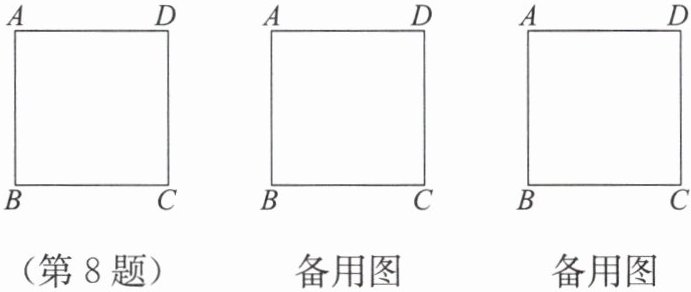
8. 如图，在边长为4的正方形ABCD中，请画出以A为一个顶点，另外两个顶点在正方形ABCD的边上，且一边长为3的所有大小不同的等腰三角形.（要求：只要画出示意图，并在所画等腰三角形长为3的边上标注数字3.）
答案：（示意图略）
解析：分情况讨论：①以A为顶点，腰长为3，分别在AB、AD、BC、CD上找点；②以A为顶点，底边长为3，分别在BC、CD上找点.共可画出6个不同的等腰三角形.
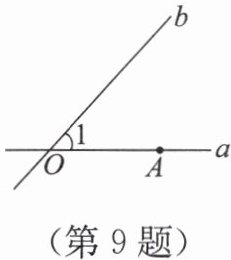
9. 如图，直线a，b相交于点O，∠1=48°，A是直线a上的定点.若B是直线b上的动点，以点O，A，B为顶点的三角形是等腰三角形，求∠OAB的度数.
答案：66°或42°或24°或84°
解析：分三种情况：①OA=OB时，∠OAB=66°或42°；②OA=AB时，∠OAB=84°；③OB=AB时，∠OAB=24°.
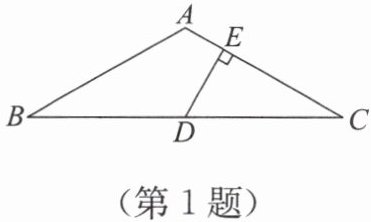
1. 如图，在△ABC中，AB=AC，∠BAC=120°，D为BC的中点，DE⊥AC，垂足为E，AE=2，求CE的长.
答案：6
解析：连接AD，AB=AC，D为BC中点，AD⊥BC，∠CAD=60°.设AD=x，在Rt△ADE中，∠DAE=60°，AE= $\frac{1}{2}$AD= $\frac{x}{2}$=2，x=4. AC= $\frac{AD}{\cos60°}$=8，CE=AC-AE=8-2=6.
