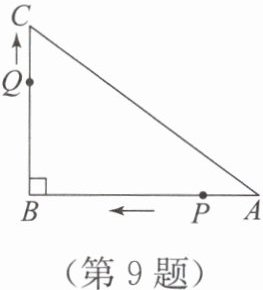
9. 如图,在△ABC 中,∠B =$90^{\circ}$,AB =
16 cm,BC = 12 cm,AC = 20 cm,P,Q 是
△ABC 边上的两个动点,其中点 P 从点 A 开
始沿 A→B 方向运动,速度为 1 cm/s,点 Q
从点 B 开始沿 B→C→A 方向运动,速度为
2 cm/s,P,Q 两点同时出发,当点 P 运动到
点 B 时两点同时停止运动,设运动时间为 t s.
(1) AP =
cm,BP =
cm.
(用含 t 的代数式表示.)
(2) 当点 Q 在边 BC 上运动时,出发几
秒后,△PQB 是等腰三角形?
(3) 当点 Q 在边 CA 上运动时,若
△BCQ 是以 BC 或 BQ 为底边的等腰三角形,
求此时 t 的值.
(第 9 题)
答案:(1) t;16 - t;(2) 16/3;(3) 11或12。
解析:
(1) t;16 - t
(2) 当点Q在BC上时,BQ=2t cm,BP=(16 - t)cm。
△PQB为等腰三角形且∠B=90°,∴BP=BQ。
即16 - t=2t,解得t=16/3。
(3) 点Q在CA上时,t>6,CQ=2(t - 6)cm。
① 以BC为底边:CQ=BQ。
设t - 6=k,则CQ=2k,Q坐标为(8k/5,12 - 6k/5),BQ=√[(8k/5)²+(12 - 6k/5)²]=2k。
平方化简得144 - 144k/5=0,k=5,t=6 + 5=11。
② 以BQ为底边:BC=CQ。
BC=12cm,∴2(t - 6)=12,t=12。
综上,t=11或12。
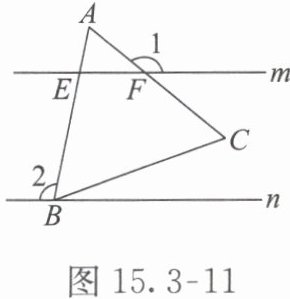
【例1】如图15.3 - 11,直线m // n,△ABC是等边三角形,顶点B在直线n上,直线m交AB于点E,交AC于点F。若∠1 = 140°,则∠2 =(
)。
A.90°
B.100°
C.110°
D.115°
解析 因为△ABC为等边三角形,
所以∠A = 60°。
因为∠1是△AEF的一个外角,所以∠1 = ∠A + ∠AEF。
所以∠AEF = ∠1 - ∠A = 140° - 60° = 80°。
所以∠BEF = 180° - ∠AEF = 180° - 80° = 100°。
因为直线m // n,
所以∠2 = ∠BEF = 100°。
答案 B
答案:B
解析:
因为△ABC为等边三角形,所以∠A = 60°。
因为∠1是△AEF的一个外角,所以∠1 = ∠A + ∠AEF。
所以∠AEF = ∠1 - ∠A = 140° - 60° = 80°。
所以∠BEF = 180° - ∠AEF = 180° - 80° = 100°。
因为直线m // n,所以∠2 = ∠BEF = 100°。