4. 如图,一辆汽车在笔直的公路 AB 上由 A 向 B 行驶,M,N 分别是位于公路 AB 两侧的村庄,当汽车行驶到哪个位置时,与村庄 M,N 的距离相等?
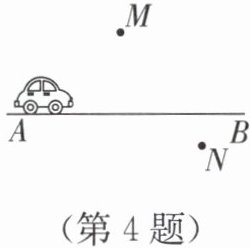
答案:设汽车行驶到点$C$时,与村庄$M$,$N$的距离相等,即$MC = NC$,
连接$MC$,$NC$,$MN$,
根据线段垂直平分线的性质,线段垂直平分线上的点到这条线段两个端点的距离相等,
所以点$C$应在线段$MN$的垂直平分线上,
而公路$AB$与村庄$M$,$N$构成平面,
所以过$M$,$N$两点作直线$MN$,再作线段$MN$的垂直平分线$l$,垂直平分线$l$与公路$AB$的交点$C$即为所求位置。
综上,当汽车行驶到线段$MN$的垂直平分线与公路$AB$的交点位置时,与村庄$M$,$N$的距离相等。
5. 如图,在△ABC 中,BC=16,AB 的垂直平分线交边 BC 于点 F,AC 的垂直平分线交边 BC 于点 H,则△AFH 的周长是(
)。
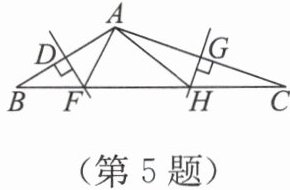
A.6
B.10
C.16
D.20
答案:C
解析:
由于 $AB$ 的垂直平分线交 $BC$ 于点 $F$,根据垂直平分线的性质,知道 $FA = FB$(垂直平分线上的点到线段的两端距离相等)。
同理,由于 $AC$ 的垂直平分线交 $BC$ 于点 $H$,可以得到 $HA = HC$。
现在,考虑三角形 $AFH$ 的周长,它由三部分组成:$AF$,$FH$,和 $HA$。
由于 $FA = FB$ 和 $HA = HC$,可以将 $AF$ 和 $HA$ 分别替换为 $FB$ 和 $HC$,得到三角形 $AFH$ 的周长为 $FB + FH + HC$。
注意到 $FB + FH + HC$ 实际上就是线段 $BC$ 的长度,即 $16$。
所以,三角形 $AFH$ 的周长为 $16$。
6. 如图,某地有两所大学和两条相交叉的公路(点 M,N 表示大学,AO,BO 表示公路)。现计划修建一座物资仓库,希望仓库到两所大学的距离相等,到两条公路的距离也相等。你能确定仓库应该建在什么位置吗?在所给的图形中画出你的设计方案。
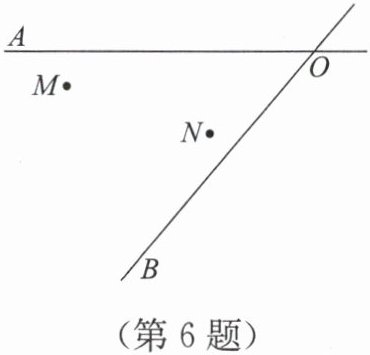
答案:1. 作两条公路 $AO$ 和 $BO$ 的角平分线 $OC$。
2. 连接两所大学 $M$ 和 $N$,并作线段 $MN$ 的垂直平分线 $EF$。
3. 垂直平分线 $EF$ 与角平分线 $OC$ 的交点 $P$ 即为仓库的位置。
在图中标出点 $P$ 的位置。
7. (创新考法) 如图,在 Rt△ABC 中,∠C=90°,∠A=30°。按下列步骤作图:分别以点 A,B 为圆心,大于 $\frac{1}{2}AB$ 的长为半径作弧,两弧相交于点 P,Q,作直线 PQ,交 AC 于点 D,交 AB 于点 E,连接 BD。下列结论:① AD=BD;② ∠CBD=30°;③ S△ABC=4S△BCD。其中正确的个数为(
)。
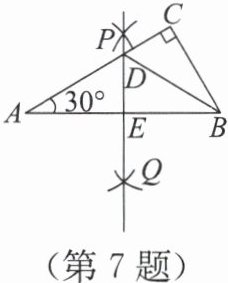
A.0
B.1
C.2
D.3
答案:C
解析:
由作图步骤知,PQ是AB的垂直平分线,故DE垂直平分AB。
①∵D在PQ上,∴AD=BD(线段垂直平分线上的点到两端距离相等),①正确;
②在Rt△ABC中,∠A=30°,∠C=90°,∴∠ABC=60°。∵AD=BD,∴∠ABD=∠A=30°,∴∠CBD=∠ABC-∠ABD=60°-30°=30°,②正确;
③设BC=x,∠A=30°,则AB=2x,AC=√3x。设CD=y,则AD=BD=√3x-y。在Rt△BCD中,BD²=BC²+CD²,即(√3x-y)²=x²+y²,解得y=x/√3。∴S△BCD=1/2·x·(x/√3)=x²/(2√3),S△ABC=1/2·√3x·x=√3x²/2,∴S△ABC=3S△BCD,③错误。
综上,正确结论为①②,共2个。
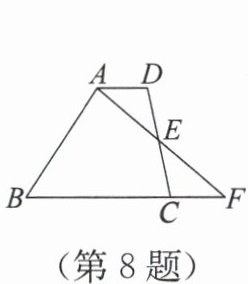
8. (运算能力) 如图,在四边形 ABCD 中,AD//BC,E 为边 CD 的中点,连接 AE,并延长 AE 交 BC 的延长线于点 F。
(1) 求证 CF=AD。
(2) 若 AD=2,AB=6,则当 BC 的长为多少时,点 B 在线段 AF 的垂直平分线上?为什么?
答案:(1)
因为 $AD // BC$,
所以 $∠ DAE = ∠ F$,$∠ D = ∠ ECF$,
因为 $E$ 是 $CD$ 的中点,
所以 $DE = CE$,
在 $△ ADE$ 和 $△ FCE$ 中,
$\begin{matrix}∠ DAE = ∠ F ,\\∠ D = ∠ ECF ,\\DE = CE.\end{matrix}$
所以 $△ ADE ≌ △ FCE$(AAS),
所以 $CF = AD$。
(2)
因为点 $B$ 在线段 $AF$ 的垂直平分线上,
所以 $AB = BF$,
因为 $AB = 6$,$AD = 2$,
由 (1) 知 $CF = AD = 2$,
所以 $BF = BC + CF = BC + 2$,
所以 $BC + 2 = 6$,
所以 $BC = 4$,
即当 $BC$ 的长为 $4$ 时,点 $B$ 在线段 $AF$ 的垂直平分线上。