【例 2】如图 15.1-12,已知△ABC 与△DFE 关于直线 l 对称,请仅用无刻度的直尺,在图 (1) 与图 (2) 中分别作出对称轴 l。
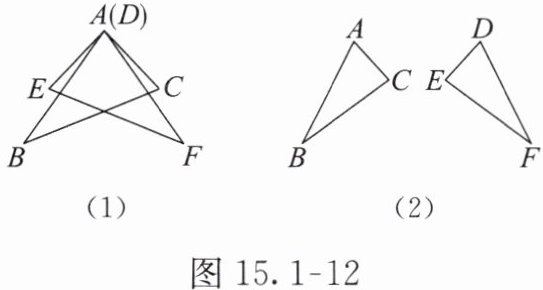
解 如图 15.1-13 (1),过 BC,EF 的交点和点 A 作直线,该直线就是所求作的直线 l。
如图 15.1-13 (2),过 BC,FE 的延长线的交点和 AC,DE 的延长线的交点作直线,该直线就是所求作的直线 l。
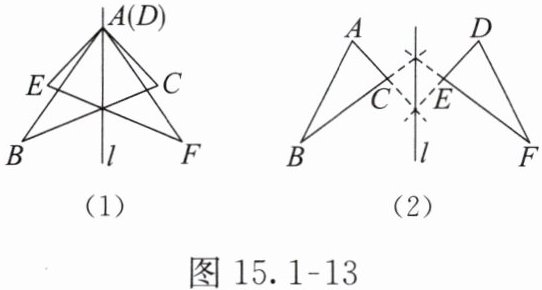
答案:图 (1):
1. 找到线段 $BC$ 和 $EF$ 的交点,记为点 $G$。
2. 通过点 $A$ 和点 $G$ 作直线 $l$。
3. 直线 $l$ 即为所求作的对称轴。
图 (2):
1. 延长线段 $BC$ 和 $FE$,找到它们的交点,记为点 $H$。
2. 延长线段 $AC$ 和 $DE$,找到它们的交点,记为点 $I$。
3. 通过点 $H$ 和点 $I$ 作直线 $l$。
4. 直线 $l$ 即为所求作的对称轴。
· 跟踪练习2 如图 15.1-14,正方形网格中的△ABC 与△DEF 成轴对称。
(1) 利用网格线作出△ABC 与△DEF 的对称轴 l;
(2) 若每一个小正方形的边长为 1,求出△ABC 的面积;
(3) 找出顶点在格点,以 BC 为一边且与△ABC 全等(不与△ABC 重合)的三角形,这样的三角形在该网格内共能画出几个?
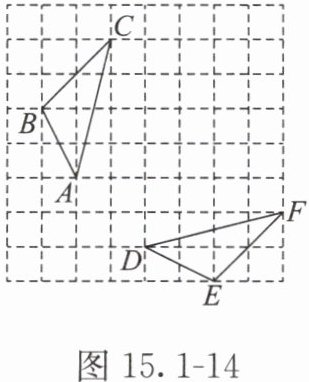
答案:(1) 如图,连接$A$和$D$,$C$和$F$(或 $B$和$E$),作出两条连接线的垂直平分线,即为对称轴 $l$。
(2) 根据网格,$△ ABC$ 的底为 3,高为 3,
面积 $S_{△ ABC} = \frac{1}{2} × 3 × 3 = \frac{9}{2} = 4.5$。
所以,该三角形面积为$4.5$。
(3) 如图,以 $BC$ 为一边,在网格内能画出与 $△ ABC$ 全等且不重合的三角形共 $5$ 个。
所以,在该网格内共能画出$5$个。
1. 如图,三座商场分别坐落在 A,B,C 所在位置,现要规划一个地铁站,使该地铁站与三座商场的距离相等,则该地铁站应建在△ABC 的(
)。

A.三条高所在直线的交点处
B.三条中线的交点处
C.三条边的垂直平分线的交点处
D.三条角平分线的交点处
答案:C
解析:
根据线段垂直平分线的性质,线段垂直平分线上的点到线段两端的距离相等。要使地铁站到A、B、C三点距离相等,需作AB、BC、AC的垂直平分线,其交点到三点距离相等,该点为△ABC三条边的垂直平分线的交点。
2. 如图,在△ABC 中,AC=6,BC=10,观察图中尺规作图的痕迹,则△ADC 的周长是(
)。
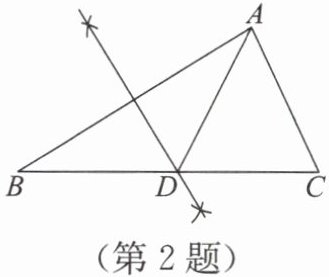
A.8
B.10
C.12
D.16
答案:D
解析:
由尺规作图痕迹可知,直线为线段AB的垂直平分线,所以AD=BD。△ADC的周长=AD+DC+AC=BD+DC+AC=BC+AC=10+6=16。
3. 如图,在△ABC 中,分别以顶点 A,B 为圆心,大于 $\frac{1}{2}AB$ 的长为半径作弧,两
弧相交于点 M,N,连接 MN,分别与边 AB,BC 相交于点 D,E。若 AC=5,△AEC 的周长为 17,则 BC=(
)。
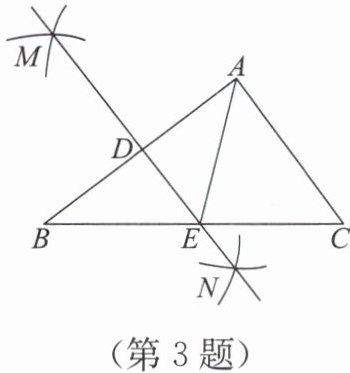
A.17
B.12
C.10
D.22
答案:B
解析:
由作图可知,MN是AB的垂直平分线,所以AE=BE。因为△AEC的周长为17,即AE+EC+AC=17,所以BE+EC+AC=17,即BC+AC=17。又因为AC=5,所以BC=17-5=12。