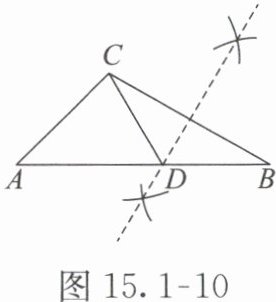
【例 1】如图 15.1-10，在△ABC 中，∠A=45°，∠B=30°。用尺规作图作边 BC 的垂直平分线，在边 AB 上确定一点 D，则∠ACD=()。


A.60°
B.70°
C.75°
D.80°
解析 由尺规作图可知，线段 BC 的垂直平分线交 AB 于点 D，记垂直平分线交 BC 于点 E(图略)，所以 DC=DB。
易证△CDE≌△BDE，所以∠DCB=∠B=30°。
因为∠ACB=180°−∠A−∠B=180°−45°−30°=105°，所以∠ACD=∠ACB−∠DCB=105°−30°=75°。
答案 C
总结 根据线段的垂直平分线的尺规作图及线段的垂直平分线的性质得到线段相等，再根据全等三角形的性质、三角形内角和定理计算即可。

· 跟踪练习1 如图 15.1-11，在△ABC 中，∠B=55°，∠C=30°，分别以点 A 和点 C 为圆心，大于 $\frac{1}{2}AC$ 的长为半径作弧，两弧相交于点 M，N，作直线 MN 交 BC 于点 D，连接 AD，则∠BAD=()。


A.50°
B.60°
C.65°
D.80°