8. 如图,$∠ ACD$是$△ ABC$的外角,$∠ BAC=80°$,$∠ ABC$和$∠ ACD$的平分线相交于点$E$,连接$AE$,则$∠ CAE=$
.
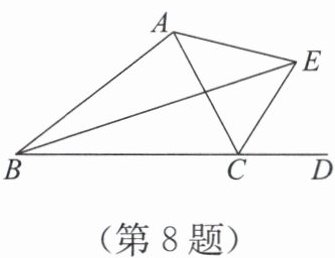
答案:50°
解析:
过点E作AB、BC、AC的垂线,垂足分别为F、G、H。
∵BE平分∠ABC,∴EF=EG(角平分线性质)。
∵CE平分∠ACD(外角),∴EG=EH(角平分线性质)。
∴EF=EH,故AE平分∠BAC的外角(到角两边距离相等的点在角平分线上)。
∠BAC=80°,其外角为180°-80°=100°,
∴∠CAE=1/2×100°=50°。
9. 如图,已知四边形$ABCD$,请用无刻度的直尺和圆规作$∠ B$的平分线$BE$,交$AD$于点$E$(不写作法,保留作图痕迹).
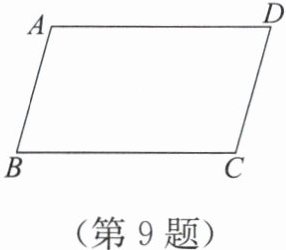
答案:①以B为圆心,任意长为半径画弧,分别交BA、BC于两点;
②分别以这两点为圆心,大于这两点间距离的一半为半径画弧,两弧交于四边形内一点F;
③作射线BF交AD于E,则BE就是所求作的∠B的平分线。
作图痕迹(用文字描述):以B为圆心作弧与BA、BC相交,再分别以两交点为圆心作弧交于四边形内一点,连接B与该交点并延长交AD于E。
10. 如图,已知$AD=AB$,$AC=AE$,$∠ DAB=∠ CAE$.
(1) 求证$△ BAE≌△ DAC$;
(2) 若$∠ CAD=126°$,$∠ D=20°$,求$∠ E$的度数.
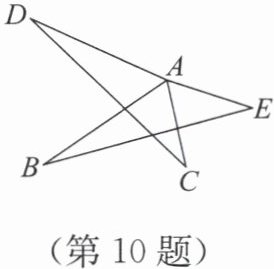
答案:(1)
证明:
∵∠DAB = ∠CAE,
∴∠DAB + ∠BAC = ∠CAE + ∠BAC,
即 ∠DAC = ∠BAE,
在△BAE和△DAC中,
AD = AB,
∠DAC = ∠BAE,
AC = AE,
∴△BAE ≌ △DAC (SAS)。
(2)
∵ ∠D = 20°,∠CAD = 126°,
∴在△DAC中,∠ACD = 180° - ∠D - ∠CAD = 180° - 20° - 126° = 34°,
∵△BAE ≌ △DAC,
∴∠E = ∠ACD,
∴∠E = 34°。
11. 如图,$△ ABC$的两条高$AD$与$BE$相交于点$O$,$AD=BD$,$AC=8$.
(1) 求$BO$的长.
(2) 设$F$是射线$BC$上一点,且$CF=AO$,动点$P$从点$O$出发,沿线段$OB$以每秒1个单位长度的速度向点$B$运动,同时动点$Q$从点$A$出发,沿射线$AC$以每秒4个单位长度的速度运动,当点$P$到达点$B$时,$P$,$Q$两点同时停止运动. 设运动时间为$t$ s,当$△ AOP$与$△ FCQ$全等时,求$t$的值.

答案:(1)8;(2)$\frac{8}{5}$或$\frac{8}{3}$.
解析:
(1)∵AD、BE是△ABC的高,∴∠ADB=∠ADC=∠BEC=90°.
∵∠OBD+∠C=90°,∠CAD+∠C=90°,∴∠OBD=∠CAD.
在△OBD和△CAD中,
$\{\begin{array}{l} ∠OBD=∠CAD \\ BD=AD \\ ∠ODB=∠ADC \end{array} $,
∴△OBD≌△CAD(ASA),∴BO=AC=8.
(2)由题意得:OP=t,AQ=4t,0≤t≤8.
∵CF=AO,∠AOP=∠ACB=∠FCQ(F在射线BC上,且F在C左侧时),∠OPA=90°(△AOP中,∠OAP+∠AOP=90°,故∠OPA=90°),
∴△AOP与△FCQ均为直角三角形,需满足OP=CQ.
①当Q在AC上(t≤2)时,CQ=AC-AQ=8-4t,
则t=8-4t,解得t=$\frac{8}{5}$.
②当Q在CA延长线上(t>2)时,CQ=AQ-AC=4t-8,
则t=4t-8,解得t=$\frac{8}{3}$.
综上,t的值为$\frac{8}{5}$或$\frac{8}{3}$.