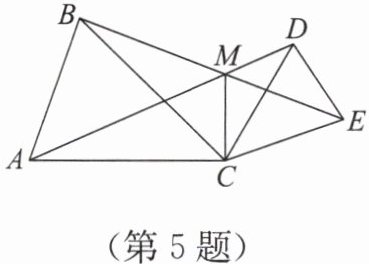
5. 如图，AC=BC，CD=CE，∠ACB=∠DCE=β，AD，BE相交于点M，连接CM.
（1）求证AD=BE；
（2）用含β的代数式表示∠AMB的度数.
答案：（1）证明：∵∠ACB=∠DCE=β，∴∠ACB+∠BCD=∠DCE+∠BCD，即∠ACD=∠BCE.在△ACD和△BCE中，AC=BC，∠ACD=∠BCE，CD=CE，∴△ACD≌△BCE（SAS），∴AD=BE.
（2）解：由（1）知△ACD≌△BCE，∴∠CAD=∠CBE.∵∠AMB=180°-∠CBE-∠ADB，∠ACB=180°-∠CAD-∠ADB，∴∠AMB=∠ACB=β.
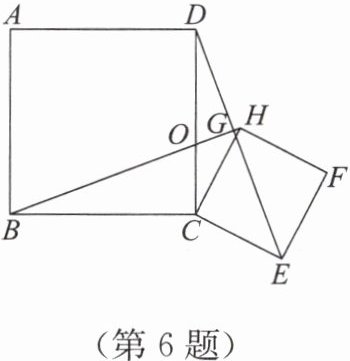
6. 如图，正方形ABCD与正方形CEFH有公共顶点C，∠BCD=∠ECH=90°，连接DE，BH，两线相交于点G，BH与CD相交于点O. 求证：
（1）BH=DE；
（2）BH⊥DE.
答案：（1）证明：∵四边形ABCD和四边形CEFH都是正方形，∴BC=CD，CH=CE，∠BCD=∠ECH=90°，∴∠BCD+∠DCH=∠ECH+∠DCH，即∠BCH=∠DCE.在△BCH和△DCE中，BC=CD，∠BCH=∠DCE，CH=CE，∴△BCH≌△DCE（SAS），∴BH=DE.
（2）证明：由（1）知△BCH≌△DCE，∴∠CBH=∠CDE.∵∠BOC=∠DOG，∠CBH+∠BOC=90°，∴∠CDE+∠DOG=90°，∴∠DGO=90°，即BH⊥DE.
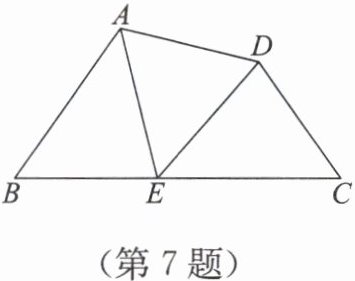
7. 如图，在四边形ABCD中，E是边BC上一点，且BE=CD，∠B=∠AED=∠C. 求证AE=ED.
答案：证明：∵∠B=∠AED=∠C，∠AEB+∠AED+∠DEC=180°，∠C+∠DEC+∠EDC=180°，∴∠AEB=∠EDC.在△ABE和△ECD中，∠B=∠C，BE=CD，∠AEB=∠EDC，∴△ABE≌△ECD（ASA），∴AE=ED.
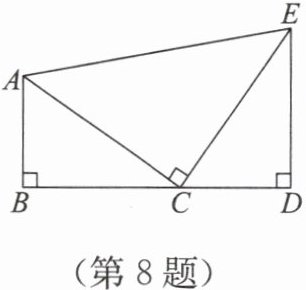
8. 如图，点B，C，D在同一条直线上，AB⊥BD，DE⊥BD，AC⊥CE，AB=CD.
（1）求证△ABC≌△CDE；
（2）若∠ACB=35°，求∠AED的度数.
答案：（1）证明：∵AB⊥BD，DE⊥BD，AC⊥CE，∴∠B=∠D=∠ACE=90°，∴∠ACB+∠ECD=90°，∠ECD+∠DEC=90°，∴∠ACB=∠DEC.在△ABC和△CDE中，∠B=∠D，∠ACB=∠DEC，AB=CD，∴△ABC≌△CDE（AAS）.
（2）解：由（1）知△ABC≌△CDE，∴AC=CE.∵∠ACE=90°，∴△ACE是等腰直角三角形，∴∠CAE=45°.∵∠BAC=90°-∠ACB=90°-35°=55°，∴∠BAE=∠BAC+∠CAE=55°+45°=100°.∵AB⊥BD，DE⊥BD，∴AB//DE，∴∠AED=180°-∠BAE=180°-100°=80°.
