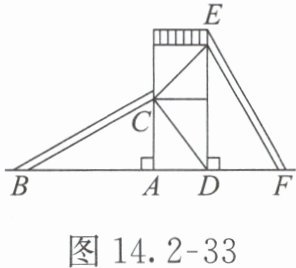
【例 2】如图 14.2-33,有两个长度相同的滑梯靠在垂直于地面的架子上,左边滑梯的高 AC 与右边滑梯水平方向的长 DF 相等。若∠CBA=36°,则∠EFD=(
)。
A.60°
B.58°
C.54°
D.48°
解析 由题意,知 AC=DF,∠BAC=∠EDF=90°。
在 Rt△ABC 和 Rt△DEF 中,
$\begin{cases} BC=EF, \\ AC=DF, \end{cases}$
所以 Rt△ABC≌Rt△DEF(HL)。
所以∠CBA=∠FED=36°。
所以∠EFD=90°-∠FED=54°。
答案 C
答案:C
解析:
由题意知,AC = DF,且∠BAC = ∠EDF = 90°。
在直角三角形 ABC 和直角三角形 DEF 中,有 BC = EF,AC = DF。
因此,直角三角形 ABC 全等于直角三角形 DEF(HL 全等)。
所以,∠CBA = ∠FED = 36°。
因此,∠EFD = 90° - ∠FED = 54°。
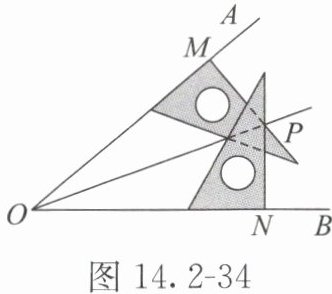
· 跟踪练习2 用三角尺画角的平分线:如图 14.2-34,先在∠AOB 的两边分别取 OM=ON,再分别过点 M,N 作 OA,OB 的垂线,交点为 P,连接 OP。得到 OP 平分∠AOB 的依据是(
)。
A.SSS
B.SAS
C.ASA
D.HL
答案:D
解析:
∵PM⊥OA,PN⊥OB,∴∠OMP=∠ONP=90°。在Rt△OMP和Rt△ONP中,OM=ON,OP=OP,∴Rt△OMP≌Rt△ONP(HL)。∴∠MOP=∠NOP,即OP平分∠AOB。
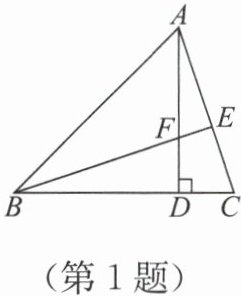
1. 如图,已知 AD 为△ABC 的高,E 为边 AC 上一点,连接 BE 交 AD 于点 F,且有 BF=AC,FD=CD,则证明△ADC≌△BDF 所用的判定方法是(
)。
A.SSS
B.AAS
C.ASA
D.HL
答案:D
解析:
∵AD为△ABC的高,∴∠ADC=∠BDF=90°。在Rt△ADC和Rt△BDF中,AC=BF,CD=FD,∴Rt△ADC≌Rt△BDF(HL)。
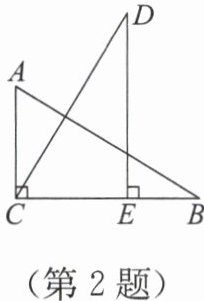
2. 如图,在 Rt△ABC 和 Rt△CDE 中,若∠ACB=∠CED=90°,AB=CD,BC=DE,则下列结论不一定正确的是(
)。
A.∠CAB=∠ECD
B.AB⊥CD
C.Rt△ABC≌Rt△CDE
D.CE=BE
答案:D
解析:
在Rt△ABC和Rt△CDE中,∠ACB=∠CED=90°,AB=CD(斜边),BC=DE(直角边),根据HL定理可得Rt△ABC≌Rt△CDE(C正确)。全等三角形对应角相等,故∠CAB=∠ECD(A正确)。由∠CAB=∠ECD,结合∠ACB=90°,可证AB⊥CD(B正确)。CE=AC(全等三角形对应边),BE=BC-CE=BC-AC,因AC与BC不一定相等,故CE=BE不一定成立(D错误)。
3. 如图,∠A=∠D=90°,点 B,E,F,C 在同一条直线上,AB=CD,BE=CF。求证∠B=∠C。
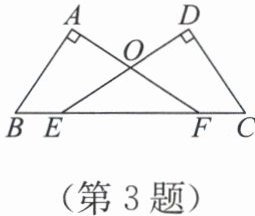
答案:证明:
∵ BE=CF,
∴ BE+EF=CF+EF,即 BF=CE。
∵ ∠A=∠D=90°,
∴ △ABF和△DCE均为直角三角形。
在Rt△ABF和Rt△DCE中,
AB=CD,
BF=CE,
∴ Rt△ABF≌Rt△DCE(HL)。
∴ ∠B=∠C。