3. 三角形的三个角的度数分别是$90°$,$60°$,$30°$,则这个三角形的形状是(
).
A.锐角三角形
B.钝角三角形
C.直角三角形
D.等腰三角形
答案:C
解析:
三角形的三个角中,有一个角为90°,根据直角三角形的定义(有一个角是直角的三角形叫做直角三角形),可知该三角形是直角三角形。
4. 三角形的分类示意图如图所示,则正确的表示是(
).
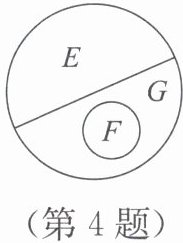
(第4题图)
A.$E$表示三边都不相等的三角形,$F$表示等腰三角形,$G$表示等边三角形
B.$E$表示三边都不相等的三角形,$F$表示等边三角形,$G$表示等腰三角形
C.$E$表示等腰三角形,$F$表示等边三角形,$G$表示三边都不相等的三角形
D.$E$表示等边三角形,$F$表示等腰三角形,$G$表示三边都不相等的三角形
答案:B
解析:
三角形按边分类可分为三边都不相等的三角形和等腰三角形,其中等边三角形是特殊的等腰三角形。图中E与G并列,F包含在G内,所以E表示三边都不相等的三角形,G表示等腰三角形,F表示等边三角形。选项B符合。
5. 下列给出的四个三角形都有一部分被遮挡,其中(
)不能按角判断出三角形类型.

A. B.
C. D.
答案:D
解析:
A中露出一个钝角,为钝角三角形;B中露出一个钝角,为钝角三角形;C中露出一个直角,为直角三角形;D中露出一个锐角,其他两角可能为锐角、直角或钝角,无法判断类型。
6. 如图,在$\bigtriangleup ABC$中,$D$,$E$分别是边$BC$,$AC$上的点,连接$BE$,$AD$相交于点$M$.
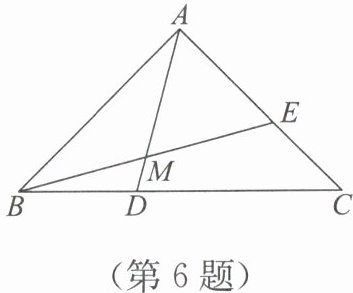
(第6题图)
(1) 图中共有多少个以$AB$为边的三角形?把它们表示出来.
(2) 除$\bigtriangleup ABM$外,以点$M$为顶点的三角形还有哪些?
(3) 若$AB = AC$,$AM = BM = EM = AE$,找出图中的等腰三角形和等边三角形.
答案:(1) 4个,分别是△ABC、△ABD、△ABE、△ABM。
(2) △AME、△BMD、△DME、△CME。
(3) 等腰三角形:△ABC、△ABM、△AME;等边三角形:△AME。
7. 如图,在$Rt \bigtriangleup ABC$中,$∠ A = 90°$,$∠ B = 30°$. 动点$P$从点$C$出发,沿边$CB$,$BA$向点$A$运动. 在点$P$运动过程中,$\bigtriangleup PAC$可能成为的特殊三角形依次是(
).
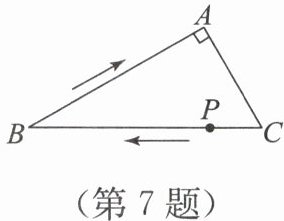
(第7题图)
A.等腰三角形→直角三角形→等边三角形→直角三角形→等腰直角三角形
B.直角三角形→等边三角形→直角三角形→等边三角形→直角三角形
C.等腰直角三角形→等腰三角形→直角三角形→等腰直角三角形→直角三角形
D.直角三角形→等边三角形→直角三角形→等腰直角三角形→直角三角形
答案:D
解析:
在$Rt△ ABC$中,$∠ A=90^{\circ}$,$∠ B=30^{\circ}$,则$∠ C=60^{\circ}$。设$AC=a$,则$BC=2a$,$AB=\sqrt{3}a$。动点$P$从$C$出发沿$CB\to BA$运动,分两段分析:
1. $P$在$CB$上运动($C\to B$):
直角三角形:当$CP=\frac{a}{2}$时,$∠ APC=90^{\circ}$,$△ PAC$为直角三角形;
等边三角形:当$CP=a$时,$CP=AC$,$∠ C=60^{\circ}$,$△ PAC$为等边三角形;
直角三角形:当$P$与$B$重合时,$∠ PAC=90^{\circ}$,$△ PAC$为直角三角形。
2. $P$在$BA$上运动($B\to A$):
等腰直角三角形:当$AP=AC=a$时,$∠ PAC=90^{\circ}$,$AP=AC$,$△ PAC$为等腰直角三角形;
直角三角形:$P$从等腰直角三角形位置向$A$运动,$∠ PAC=90^{\circ}$始终成立,$△ PAC$为直角三角形。
依次为:直角三角形→等边三角形→直角三角形→等腰直角三角形→直角三角形。