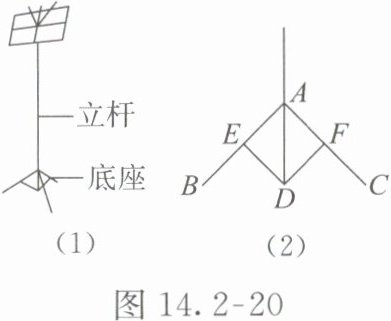
跟踪练习2 图14.2-20（1）是一乐谱架示意图，利用立杆可进行高度调节；图14.2-20（2）是乐谱架底座部分的平面图，其中支撑杆AB=AC，E，F分别为AB，AC的中点，ED，FD是连接立杆和支撑杆的支架，且ED=FD. 立杆在伸缩过程中，总有△AED≌△AFD，其判定依据是（ ）.
A. SSS B. SAS C. ASA D. AAS
答案：A
解析：∵E、F为中点，∴AE=AF。又AD=AD，ED=FD，∴△AED≌△AFD（SSS），选A。
1. 如图，在△ABC中，AB=AC，EB=EC，直接使用“SSS”可判定（ ）.
A. △ABE≌△EDC B. △ABE≌△ACE C. △BED≌△CED D. △ABD≌△ACD
答案：B
解析：在△ABE和△ACE中，AB=AC，EB=EC，AE=AE，∴△ABE≌△ACE（SSS），选B。
2. 根据下列已知条件，不能画出唯一△ABC的是（ ）.
A. AB=6，∠B=50°，BC=8 B. AB=6，BC=7，CA=8
C. AB=4，BC=3，∠A=40° D. ∠A=60°，∠B=40°，AB=8
答案：C
解析：C选项为SSA，不能唯一确定三角形，选C。
3. 如图，AB=AC，AD=AE，BD=CE，BD与CE相交于点O，与∠CAB（不包括∠CAB）一定相等的角有（ ）.
A. 4个 B. 3个 C. 2个 D. 1个
答案：B
解析：△ABD≌△ACE（SSS），得∠ABD=∠ACE，∠ADB=∠AEC，∠BAD=∠CAE，进而可得∠BOC=∠CAB，共3个角，选B。
4. 如图，点A，D，B，E在同一条直线上，已知AD=BE，AC=DF，BC=EF. 若∠A=70°，∠E=60°，则∠C=（ ）.
A. 35° B. 40° C. 45° D. 50°
答案：D
解析：∵AD=BE，∴AB=DE。在△ABC和△DEF中，AB=DE，AC=DF，BC=EF，∴△ABC≌△DEF（SSS），∴∠C=∠F=180°-∠A-∠B=180°-70°-60°=50°，选D。
5. 请你把下面这道题的解答过程补充完整.
如图，已知AE=DE，EB=EC，AB=DC，∠ACB=30°. 求∠DBC的度数.
答案：30°
证明：在△AEB和△DEC中，AE=DE，EB=EC，AB=DC，∴△AEB≌△DEC（SSS），∴∠ABE=∠DCE。在△ABC和△DCB中，AB=DC，AC=DB（由△AEB≌△DEC得AC=DB），BC=CB，∴△ABC≌△DCB（SSS），∴∠ACB=∠DBC=30°。
