【例 2】如图 14.2-5,在 3×3 的正方形网格中,每个小正方形的边长都为 1,则∠1 和∠2 的关系为(
)。
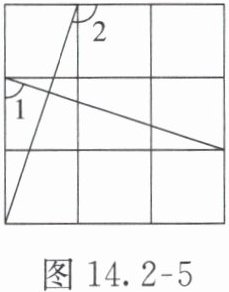
A.∠1+∠2=180°
B.∠2=2∠1
C.∠1+90°=∠2
D.∠1=∠2
解析 如图 14.2-6。
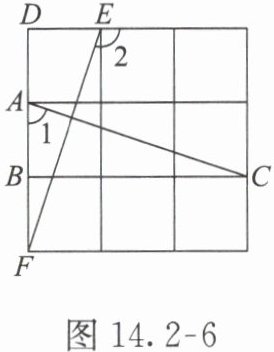
由已知条件,得 AB=ED,BC=DF,∠ABC=∠EDF=90°,所以△ABC≌△EDF(SAS),所以∠1=∠DEF,所以∠1+∠2=180°。
答案 A
答案:A
解析:
如图,设网格中相关点为A、B、C、D、E、F。由网格性质得AB=ED,BC=DF,∠ABC=∠EDF=90°,则△ABC≌△EDF(SAS),故∠1=∠DEF。又∠DEF+∠2=180°,所以∠1+∠2=180°。
· 跟踪练习2 某数学兴趣小组学完三角形全等的判定后,自编如下试题:如图 14.2-7,△ABC 是格点三角形(顶点在网格线的交点即格点上),请在下列每个网格纸上按要求各画一个与△ABC 全等的格点三角形。
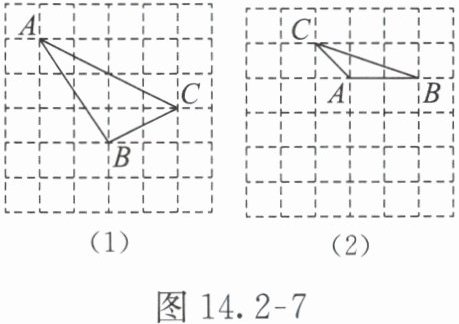
(1) 在图 14.2-7(1)中所画三角形与△ABC 有一个公共角∠C;
(2) 在图 14.2-7(2)中所画三角形与△ABC 有且只有一个公共顶点 A。
答案:(1) 使用直尺,以点 $C$ 为公共角顶点,作 $△A'B'C$,使 $A'$ 和 $B'$ 位于网格点上,且 $A'C = AC$,$B'C = BC$,$A'B' = AB$。
检查:通过 $SSS$ 或 $SAS$ 全等条件验证 $△A'B'C ≌ △ABC$。
(2) 在图 (2) 中,使用直尺,以点 $A$ 为公共顶点,作 $△A'B'C'$,使 $A'$(即 $A$)位于网格点上,且 $A'B' = AB$,$A'C' = AC$,$B'C' = BC$。
检查:通过 $SSS$ 全等条件验证 $△A'B'C' ≌ △ABC$。
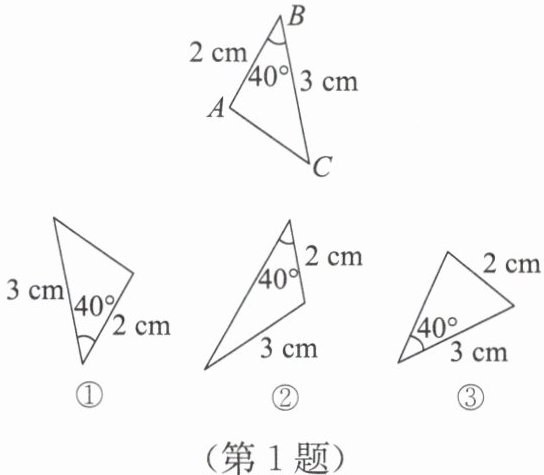
1. 下列图形中与△ABC 全等的是(
)。
A.①③
B.①②
C.②③
D.只有①
答案:A
解析:
根据题意,已知$△ ABC$的边$AB=2\mathrm{cm}$,$AC=3\mathrm{cm}$,$∠ A=40°$,
如图,图形①,边长为$3\mathrm{cm}$和$2\mathrm{cm}$,其夹角为$40°$,与$△ ABC$对应边和对应角相等,符合$SAS$;
图形②,边长为$2\mathrm{cm}$的边其邻边为$3\mathrm{cm}$,但角不对应相等,故不符合;
图形③,边长为$3\mathrm{cm}$和$2\mathrm{cm}$,其夹角为$40°$,与$△ ABC$对应边和对应角相等,符合$SAS$;
所以与$△ ABC$全等的是图形①和图形③。
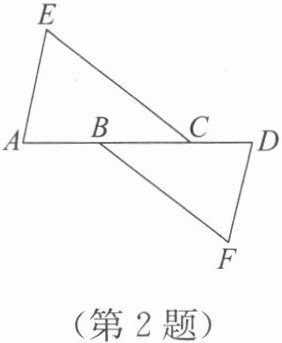
2. 如图,AE//DF,AE=DF,若要使△EAC≌△FDB,则可添加条件(
)。
A.∠A=∠D
B.AB=CD
C.∠E=∠DBF
D.AC=BF
答案:B
解析:
已知$ AE // DF $,所以$∠ A = ∠ D$(两直线平行,内错角相等)。
又已知$ AE = DF $,要使$ △ EAC ≌ △ FDB $,需要满足边角边(SAS)条件。
现在已经有$ ∠ A = ∠ D $和$ AE = DF $,只需添加$ AB = CD $,则$ AC = DB $(因为$ AC = AB + BC $,$ DB = CD + BC $,且$ AB = CD $)。
因此,可以得出$ △ EAC ≌ △ FDB $。
所以选择B。