1. 若一个三角形的两边长分别为 3 和 7,则第三边长可能是(
).
A.3
B.4
C.6
D.10
答案:C
解析:
设第三边的长为x,根据三角形两边之和大于第三边,两边之差小于第三边,可得:
$7 - 3 < x < 7 + 3$,
即$4 < x < 10$,
只有选项C中的6满足该范围。
2. △ABC 的三个内角的度数之比是 1∶2∶3,则△ABC 是(
).
A.锐角三角形
B.钝角三角形
C.直角三角形
D.无法确定
答案:C
解析:
设三角形的三个内角的度数分别为 $x$,$2x$,$3x$。
根据三角形内角和定理,三角形的三个内角之和为$180 ^{\circ}$,
所以,$x + 2x + 3x = 180 ^{\circ}$,
合并同类项得:
$6x = 180 ^{\circ}$
系数化为$1$得:
$x = 30 ^{\circ}$
所以三角形的三个内角分别为:
$30 ^{\circ}$,$60 ^{\circ}$,$90 ^{\circ}$。
由于其中一个角为$90 ^{\circ}$,所以$\bigtriangleup ABC$是直角三角形。
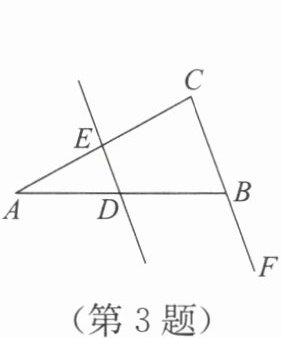
3. 如图,BC//DE,∠ABF=110°,∠AED=80°,则∠A=(
).
A.30°
B.35°
C.40°
D.45°
答案:A
解析:
∵∠ABF=110°,∠ABF+∠ABC=180°(平角定义),∴∠ABC=180°-110°=70°.
∵BC//DE,∴∠ACB=∠AED=80°(两直线平行,同位角相等).
在△ABC中,∠A+∠ABC+∠ACB=180°(三角形内角和定理),
∴∠A=180°-∠ABC-∠ACB=180°-70°-80°=30°.
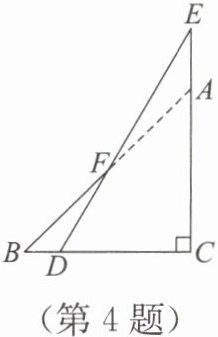
4. 将一副三角尺按如图所示的位置叠放,其中∠C=90°,∠B=45°,∠E=30°,则∠BFD=(
).
A.30°
B.25°
C.20°
D.15°
答案:D
解析:
在等腰直角△ABC中,∠C=90°,∠B=45°,故∠A=45°。含30°角的直角三角尺中,∠E=30°,则另一个锐角∠EDC=60°(直角三角形两锐角互余)。由图可知点D在BC延长线上,故∠BDF=180°-∠EDC=180°-60°=120°。在△BDF中,∠BFD=180°-∠B-∠BDF=180°-45°-120°=15°。
5. 在△ABC 中,BC=6,边 BC 上的高 AD=3,BD=2,则△ACD 的面积是(
).
A.12
B.6
C.6 或 12
D.以上都不对
答案:C
解析:
AD是BC边上的高,AD=3,分两种情况:
①当D在BC上(B、C之间)时,BC=6,BD=2,∴DC=BC-BD=6-2=4,S△ACD=1/2×DC×AD=1/2×4×3=6;
②当D在BC延长线上(B在D、C之间)时,BD=2,BC=6,∴DC=BD+BC=2+6=8,S△ACD=1/2×DC×AD=1/2×8×3=12。
综上,△ACD面积是6或12。
6. 已知实数 a,b 满足|a−5|+(b−9)²=0,则以 a,b,c 为边长的三角形中 c 的取值范围是
.
答案:$4 < c < 14$(写最终范围即可,不用写其他内容)。
解析:
由题意,已知 $|a - 5| + (b - 9)^{2} = 0$。
因为绝对值和平方均非负,所以要使上式成立,必须有 $|a - 5| = 0$ 和 $(b - 9)^{2} = 0$。
解得 $a = 5$,$b = 9$。
根据三角形的三边关系,两边之和大于第三边,两边之差小于第三边,即:
$a + b > c$,$|a - b| < c$,$a+c>b$(由于a小于b,该式必然满足),
将 $a = 5$,$b = 9$代入,得到:
$c < 5 + 9$,$c > |5 - 9|$,
即:$c < 14$,$c > 4$。
所以,$4 < c < 14$。
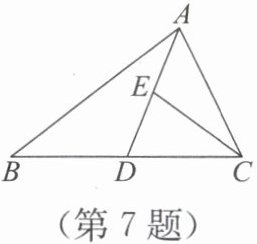
7. 如图,在△ABC 中,D,E 分别为 BC,AD 的中点. 若 S△AEC=2,则 S△ABC=
.
答案:8
解析:
∵E为AD中点,∴AE=DE,∴S△AEC=S△DEC=2(等底同高),∴S△ADC=S△AEC+S△DEC=4.∵D为BC中点,∴BD=CD,∴S△ABD=S△ADC=4(等底同高),∴S△ABC=S△ABD+S△ADC=8.
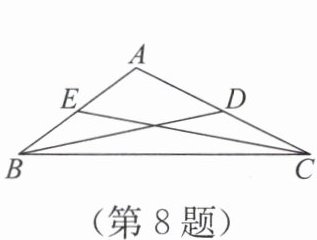
8. 如图,在△ABC 中,若 CD= $\frac{1}{3}$ BC=4,BE= $\frac{1}{4}$ BC,BD,CE 是△ABC 的两条中线,则△ABC 的周长是
.
答案:26
解析:
∵CD=1/3 BC=4,∴BC=12。∵BE=1/4 BC,∴BE=1/4×12=3。∵BD,CE是中线,∴D是AC中点,E是AB中点。∴AC=2CD=2×4=8,AB=2BE=2×3=6。∴△ABC周长=AB+BC+AC=6+12+8=26。
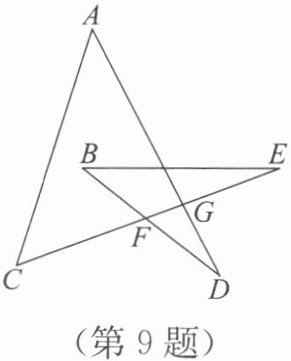
9. 如图,∠A+∠B+∠C+∠D+∠E=
.
答案:180°
解析:
连接BC,设BD与CE交于点O。在△ODE中,∠D+∠E+∠DOE=180°;在△OBC中,∠OBC+∠OCB+∠BOC=180°。∵∠DOE=∠BOC(对顶角相等),∴∠D+∠E=∠OBC+∠OCB。则∠A+∠B+∠C+∠D+∠E=∠A+∠ABE+∠ACD+∠OBC+∠OCB=∠A+(∠ABE+∠OBC)+(∠ACD+∠OCB)=∠A+∠ABC+∠ACB=180°(三角形内角和定理)。
10. 如图,AB//CD,AE 交 CD 于点 F. 若∠A=65°,∠C=25°,则∠E=
.

答案:$40°$
解析:
由于 $AB // CD$,且 $ ∠ A = 65° $,根据平行线的性质,$ ∠ EFD = ∠ A = 65° $。
在三角形 $ CEF $ 中,已知 $ ∠ C = 25° $ 和 $ ∠ EFD = 65° $。
根据三角形的外角定理,$ ∠ EFD = ∠ C + ∠ E $。
因此,$ ∠ E = ∠ EFD - ∠ C = 65° - 25° = 40° $。