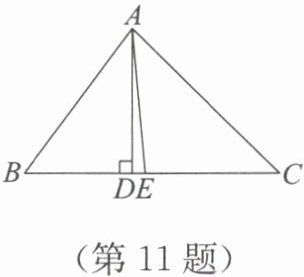
11. 如图,在△ABC 中,∠BAC=82°,AD⊥BC,垂足为 D,AE 平分∠BAC,∠B=54°,求∠DAE 的度数.
答案:在$△ ABC$中,
$\because ∠ BAC = 82°, ∠ B = 54°$,
$\therefore ∠ C = 180° - ∠ BAC - ∠ B = 180° - 82° - 54° = 44°$。
$\because AE$平分$∠ BAC$,
$\therefore ∠ BAE = \frac{1}{2} ∠ BAC = \frac{1}{2} × 82° = 41°$。
$\because AD ⊥ BC$,
$\therefore ∠ ADC = 90°$,
$\therefore$在$△ ADC$中,
$∠ CAD = 180° - ∠ ADC - ∠ C = 180° - 90° - 44° = 46°$。
$\therefore ∠ DAE = ∠ CAD - ∠ CAE = 46° - 41° = 5° \mspace{2mu}$(或$∠ DAE = ∠ BAE - ∠ BAD,∠ BAD = 90° - ∠ B = 36°,∠ DAE = 41° - 36° = 5°$)。
$\therefore ∠ DAE = 5° \mspace{2mu} 18$
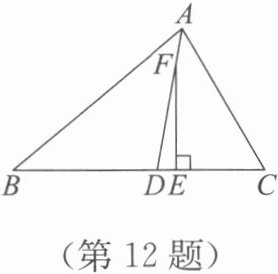
12. 如图,已知在△ABC 中,∠B<∠C,AD 平分∠BAC,F 是线段 AD(除去端点 A,D)上一动点,EF⊥BC,垂足为 E.
(1)若∠B=40°,∠DFE=10°,求∠C 的度数;
(2)若∠B=α,∠C=β,请用含 α,β 的代数式表示∠DFE 的度数.
答案:(1)∵EF⊥BC,∴∠FED=90°.
在Rt△FED中,∠DFE=10°,∴∠FDE=90°-∠DFE=80°.
设∠BAC=2x,∵AD平分∠BAC,∴∠BAD=∠CAD=x.
在△ABC中,∠B+∠C+∠BAC=180°,∠B=40°,∴∠C=140°-2x.
在△ADC中,∠ADC=180°-∠C-∠CAD=180°-(140°-2x)-x=40°+x.
∵∠FDE=∠ADC,∴40°+x=80°,解得x=40°.
∴∠BAC=2x=80°,∠C=180°-∠B-∠BAC=180°-40°-80°=60°.
(2)∠DFE=(β-α)/2.
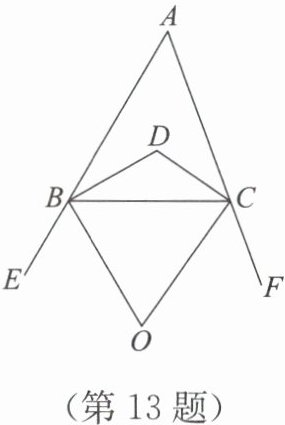
13. 如图,BD,CD 分别是∠ABC,∠ACB 的平分线,BO,CO 分别是△ABC 的外角∠CBE,∠BCF 的平分线.
(1)当∠ABC=62°,∠ACB=68°时,求∠D,∠O 的度数.
(2)当∠A=48°时,求∠D 和∠O 的度数.
(3)当∠A 的大小变化时,∠D+∠O 的值是否变化?请说明理由.
答案:(1)∵BD,CD分别平分∠ABC,∠ACB,∠ABC=62°,∠ACB=68°,
∴∠DBC=1/2∠ABC=31°,∠DCB=1/2∠ACB=34°,
∴∠D=180°-∠DBC-∠DCB=180°-31°-34°=115°;
∵∠CBE=180°-∠ABC=118°,∠BCF=180°-∠ACB=112°,BO,CO分别平分∠CBE,∠BCF,
∴∠OBC=1/2∠CBE=59°,∠OCB=1/2∠BCF=56°,
∴∠O=180°-∠OBC-∠OCB=180°-59°-56°=65°。
(2)∵∠A=48°,∴∠ABC+∠ACB=180°-∠A=132°,
∵BD,CD分别平分∠ABC,∠ACB,
∴∠DBC+∠DCB=1/2(∠ABC+∠ACB)=66°,
∴∠D=180°-66°=114°;
∵∠CBE+∠BCF=360°-(∠ABC+∠ACB)=228°,BO,CO分别平分∠CBE,∠BCF,
∴∠OBC+∠OCB=1/2(∠CBE+∠BCF)=114°,
∴∠O=180°-114°=66°。
(3)不变,理由如下:
∠D=90°+1/2∠A,∠O=90°-1/2∠A,
∴∠D+∠O=180°,为定值。