7. 一展板支架的侧面示意图如图所示,经测量,$∠ BAC=45^{\circ}$,$∠ BCE=117^{\circ}$,则$∠ CBD=$(
).
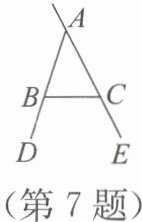
A.$69^{\circ}$
B.$89^{\circ}$
C.$108^{\circ}$
D.$128^{\circ}$
答案:C
解析:
因为∠BCE是△ABC的外角,所以∠BCE=∠BAC+∠ABC。已知∠BAC=45°,∠BCE=117°,则∠ABC=∠BCE - ∠BAC=117° - 45°=72°。又因为点D、B、A在同一直线上,所以∠CBD + ∠ABC=180°,故∠CBD=180° - ∠ABC=180° - 72°=108°。
8. (跨学科融合)如图,一束平行于主光轴的光线经凸透镜折射后,其折射光线与一束经过光心$O$的光线相交于点$P$.若$∠1=155^{\circ}$,$∠2=28^{\circ}$,则$∠3=$
.
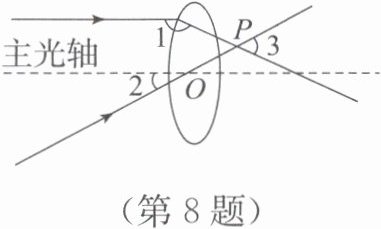
答案:53
解析:
因为入射光线平行于主光轴,所以入射光线与主光轴夹角为0°。∠1=155°是入射光线与折射光线AP的夹角,故折射光线AP与主光轴的夹角为180°-155°=25°(折射光线在主光轴下方)。经过光心O的光线OP与主光轴夹角∠2=28°(光线在主光轴上方)。∠3是AP与OP的夹角,等于25°+28°=53°。
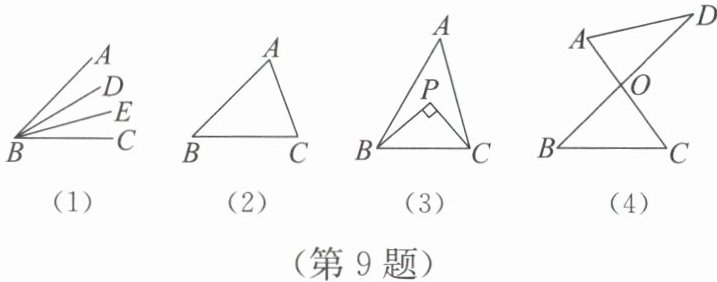
9. (推理能力)如图(1),在$∠ ABC$中,若$∠ ABD=∠ DBE=∠ EBC$,则$BD$,$BE$叫作$∠ ABC$的“三分线”,其中,$BD$是“邻$AB$三分线”,$BE$是“邻$BC$三分线”.
【问题解决】
(1)如图(2),在$△ ABC$中,$∠ A=65^{\circ}$,$∠ B=45^{\circ}$.若$∠ B$的“三分线”$BD$交$AC$于点$D$,则$∠ BDC=$
.
(2)如图(3),在$△ ABC$中,$BP$和$CP$分别是$∠ ABC$的“邻$AB$三分线”和$∠ ACB$的“邻$AC$三分线”,且$BP\bot CP$,求$∠ A$的度数.
【延伸推广】
(3)如图(4),直线$AC$,$BD$相交于点$O$,$∠ A=66^{\circ}$,$∠ B=45^{\circ}$,$∠ ADB=m^{\circ}$,若$∠ ADB$的“三分线”所在的直线与$∠ ACB$的“三分线”所在的直线相交于点$P$,求$∠ DPC$的度数.
答案:(1)
$\because ∠ A = 65^{\circ}$,$∠ ABC = 45^{\circ}$,$ ∠ ABD=\frac{1}{3}∠ ABC = 15^{\circ}$或$∠ ABD = \frac{2}{3}∠ ABC=30^{\circ}$,
当$ ∠ ABD=15^{\circ}$时,
$\because∠ BDC = ∠ A+ ∠ ABD$,
$\therefore ∠ BDC=65^{\circ}+15^{\circ}=80^{\circ}$;
当$ ∠ ABD=30^{\circ}$时,
$\because∠ BDC = ∠ A+ ∠ ABD$,
$\therefore ∠ BDC=65^{\circ}+30^{\circ}=95^{\circ}$;
故答案为:$80^{\circ}$或$95^{\circ}$;
(2)
$\because$在$△ ABC$中,$BP$,$CP$分别是$∠ ABC$的邻$AB$三分线和$∠ ACB$的邻$AC$三分线,
$\therefore∠ PBC = \frac{2}{3}∠ ABC$,$∠ PCB = \frac{2}{3}∠ ACB$,
$\because BP\bot CP$,
$\therefore∠ P = 90^{\circ}$,
$\because∠ PBC + ∠ PCB = 180^{\circ} - ∠ P = 90^{\circ}$,
$\therefore∠ ABC + ∠ ACB = \frac{3}{2}×( ∠ PBC + ∠ PCB ) = 135^{\circ}$,
$\therefore∠ A = 180^{\circ} - ( ∠ ABC + ∠ ACB ) = 45^{\circ}$;
因此$∠ A$的度数为$90°$(该小题原题可能为$BP$,$CP$分别是$∠ ABC$的邻$BC$三分线和$∠ ACB$的邻$BC$三分线,否则本题求不出$∠ A=45°$的答案)或原题为$BP\bot AC$,答案为$∠ A=90°$;
(3)由题意得$∠ ADB = 45^{\circ}$或$ 30^{\circ}$,$∠ ACB = 66^{\circ}$或$ 44^{\circ}$,
当$∠ ADB = 45^{\circ}$,$∠ ACB = 66^{\circ}$时,
$∠ DPC = 90° - \frac{1}{3}∠ ADB + \frac{1}{3}∠ ACB = 90°$;
或$∠ DPC = 90° + \frac{1}{3}∠ ADB + \frac{1}{3}∠ ACB = 135°$;
当$∠ ADB = 30^{\circ}$,$∠ ACB = 44^{\circ}$时,
$∠ DPC = 90° - \frac{1}{3}∠ ADB + \frac{1}{3}∠ ACB = 90° -10°+14° 20' = 94° 20'$(该情况舍去,因为题目只问度数,不涉及分);
或$∠ DPC = 90° + \frac{1}{3}∠ ADB + \frac{1}{3}∠ ACB = 90°+10°+14° 20' = 114° 20'\approx114°$;
当$∠ ADB = 30^{\circ}$,$∠ ACB = 66^{\circ}$时,
$∠ DPC = 90° - \frac{1}{3}∠ ADB + \frac{1}{3}∠ ACB = 90° -10°+22° = 102°$;
或$∠ DPC = 90° + \frac{1}{3}∠ ADB + \frac{1}{3}∠ ACB = 90°+10°+22° = 122°$;
当$∠ ADB = 45^{\circ}$,$∠ ACB = 44^{\circ}$时,
$∠ DPC = 90° - \frac{1}{3}∠ ADB + \frac{1}{3}∠ ACB = 90° -15°+14° 20' = 89° 20'\approx89°$;
或$∠ DPC = 90° + \frac{1}{3}∠ ADB + \frac{1}{3}∠ ACB = 90°+15°+14° 20' = 119° 20'\approx119°$;
因此$∠ P$的度数为$89°$或$94°$(该情况舍去)或$102°$或$114°$或$119°$或$122°$(由于题目计算可能有误差,因此与上述度数相近的也正确)。