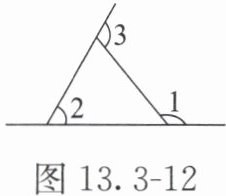
跟踪练习2 一天,李明和爸爸一起到建筑工地去,看见了一个人字梯(示意图如图13.3-12所示),爸爸说:“李明,我考考你,如果这个人字梯中的$∠3=110^{\circ}$,你能求出$∠1$比$∠2$大多少吗?”请你帮李明计算一下,正确的答案是(
).
A.$80^{\circ}$
B.$70^{\circ}$
C.$60^{\circ}$
D.$50^{\circ}$
答案:B
解析:
设∠3的邻补角为∠4,则∠3+∠4=180°,∠4=180°-110°=70°。∠1是三角形的外角,∠1=∠2+∠4,故∠1-∠2=∠4=70°。
1. 如图,点$D$在线段$BC$的延长线上,过点$B$作射线$BF$,交$AC$于点$E$,则下列角是$△ ABE$的外角的是(
).
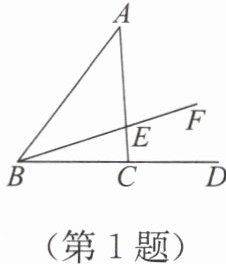
A.$∠ AEF$
B.$∠ CBE$
C.$∠ ACD$
D.$∠ CEF$
答案:A
解析:
根据三角形外角的定义,三角形的一边与另一边的延长线组成的角叫做三角形的外角。对于△ABE,其外角应是由三角形的一边延长后与另一边组成的角。
选项A:∠AEF,是△ABE的边AE的延长线与边BE组成的角,符合外角定义。
选项B:∠CBE是△BCE的内角,不是△ABE的外角。
选项C:∠ACD是△ABC的外角,与△ABE无关。
选项D:∠CEF是△BCE的内角,不是△ABE的外角。
综上,是△ABE外角的是∠AEF。
2. 如图,已知$∠ ACD=120^{\circ}$,$∠ B=20^{\circ}$,则$∠ A=$(
).
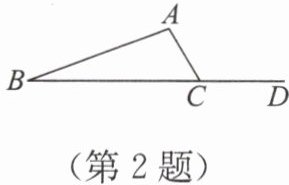
A.$120^{\circ}$
B.$110^{\circ}$
C.$100^{\circ}$
D.$30^{\circ}$
答案:C
解析:
根据三角形的外角性质,三角形的一个外角等于与它不相邻的两个内角之和。在题目中,$∠ ACD$ 是三角形 $ABC$ 的一个外角,因此有:
$∠ ACD = ∠ A + ∠ B$,
给定 $∠ ACD = 120°$ 和 $∠ B = 20°$,代入上式得:
$120° = ∠ A + 20°$,
解这个方程,得到:
$∠ A = 100°$。
故答案为C。
3. 将一副三角尺按如图所示的位置叠放,则$∠ CBE=$(
).
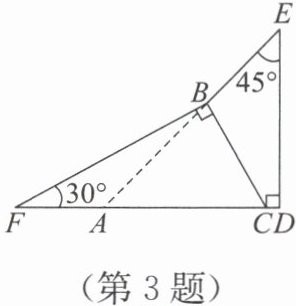
A.$110^{\circ}$
B.$105^{\circ}$
C.$100^{\circ}$
D.$90^{\circ}$
答案:B
解析:
由图可知,含30°角的三角尺中∠F=30°,∠FAB=90°,含45°角的三角尺中∠E=45°,∠EDC=90°。因为∠FAB=90°,∠F=30°,所以∠FBA=180°-90°-30°=60°。又因为∠FBA+∠ABC=180°(平角定义),所以∠ABC=180°-60°=120°。在含45°角的三角尺中,∠EBC=45°,所以∠CBE=∠ABC-∠EBC=120°-15°=105°。
4. 如图,$BE$为$△ ABC$的外角$∠ CBD$的平分线.若$∠ A=50^{\circ}$,$∠ C=62^{\circ}$,则$∠ EBD=$(
).
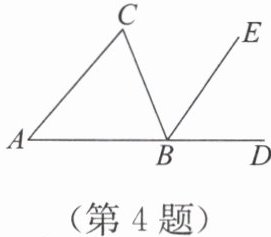
A.$50^{\circ}$
B.$56^{\circ}$
C.$60^{\circ}$
D.$65^{\circ}$
答案:B
解析:
已知$∠ A=50^{\circ}$,$∠ C=62^{\circ}$,根据三角形内角和为$180^{\circ}$,可得$∠ ABC = 180^{\circ}-∠ A - ∠ C=180^{\circ}-50^{\circ}-62^{\circ}=68^{\circ}$。
那么$△ ABC$的外角$∠ CBD$的度数为$180^{\circ}-∠ ABC = 180^{\circ}- 68^{\circ}=112^{\circ}$。
因为$BE$是$∠ CBD$的平分线,所以$∠ EBD=\frac{1}{2}∠ CBD=\frac{1}{2}×112^{\circ}=56^{\circ}$。
5. 小华在上数学课时看到同桌将一副三角尺按如图所示的位置叠放,则$∠ AOB=$
.
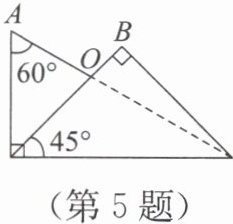
答案:75°
解析:
由图可知,含30°角的直角三角尺中,∠ACO=90°,∠A=60°,则∠AOC=180°-90°-60°=30°;含45°角的直角三角尺中,∠BCO=45°,∠B=90°,则∠BOC=180°-90°-45°=45°。因为∠AOB=∠AOC+∠BOC,所以∠AOB=30°+45°=75°。
6. 如图,$CE$是$△ ABC$的外角$∠ ACD$的平分线,且$CE$交$BA$的延长线于点$E$.
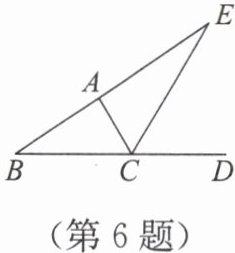
(1)若$∠ B=35^{\circ}$,$∠ E=25^{\circ}$,求$∠ BAC$的度数;
(2)探究$∠ BAC$,$∠ B$,$∠ E$之间的数量关系,并说明理由.
答案:(1)∵CE是∠ACD的平分线,∴∠ACE=∠ECD。
∵∠ACD是△ABC的外角,∴∠ACD=∠B+∠BAC,∴∠ECD=1/2∠ACD=1/2(∠B+∠BAC)。
∵∠ECD是△BCE的外角,∴∠ECD=∠B+∠E。
∴1/2(∠B+∠BAC)=∠B+∠E。
∵∠B=35°,∠E=25°,∴1/2(35°+∠BAC)=35°+25°,解得∠BAC=85°。
(2)∠BAC=∠B+2∠E。
理由:∵CE平分∠ACD,∴∠ECD=1/2∠ACD。
∵∠ACD=∠B+∠BAC,∴∠ECD=1/2(∠B+∠BAC)。
∵∠ECD=∠B+∠E,∴1/2(∠B+∠BAC)=∠B+∠E,∴∠BAC=∠B+2∠E。