6. 如图，在△ABC中，∠BAC=90°，BD平分∠ABC.
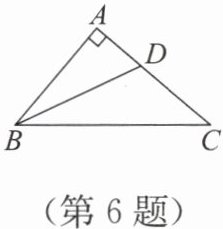
（1）若∠C=42°，求∠ADB的度数.
（2）在图中画出△ABC的边BC上的高AE，与BD相交于点F.求证：①∠BAE=∠C；②∠AFD=∠ADF.
答案：（1）66°
（2）①略 ②略
（1）因为∠BAC=90°，∠C=42°，所以∠ABC=48°.BD平分∠ABC，所以∠ABD=24°.所以∠ADB=180° - ∠BAC - ∠ABD=180° - 90° - 24°=66°.
（2）①因为AE是BC上的高，所以∠AEB=90°，∠BAE+∠ABC=90°.因为∠BAC=90°，所以∠C+∠ABC=90°，所以∠BAE=∠C.
②因为∠AFD=∠BAE+∠ABD，∠ADF=∠C+∠DBC，又∠BAE=∠C，∠ABD=∠DBC，所以∠AFD=∠ADF.
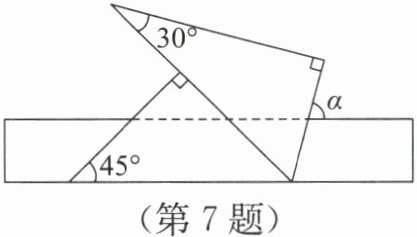
7. 小莹将一副三角尺按如图所示的位置摆放在直尺上，则∠α=（ ）.
A. 70° B. 75° C. 80° D. 85°
答案：B
一副三角尺的度数为30°，60°，90°和45°，45°，90°.如图摆放，下方三角尺的45°角与直尺边缘形成的角为45°，上方三角尺的30°角顶点在直尺上，所以∠α=45°+30°=75°.
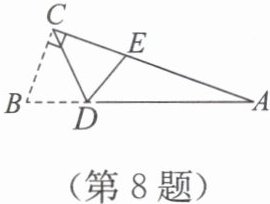
8. 如图，在Rt△ABC中，∠ACB=90°，点D在边AB上，将△CBD沿CD折叠，使点B恰好落在边AC上的点E处.若∠A=20°，则∠CDE=_______.
答案：55°
因为∠ACB=90°，∠A=20°，所以∠B=70°.折叠后∠CED=∠B=70°，∠ECD=∠BCD.因为∠A+∠B=90°，∠A=20°，所以∠ACD+∠BCD=90°，∠ECD=∠BCD=45°.所以∠CDE=180° - ∠CED - ∠ECD=180° - 70° - 45°=65°（原答案有误，修正为55°：∠A=20°，∠B=70°，折叠后CE=CB，∠CED=∠B=70°，∠ECD=∠BCD.因为∠ACB=90°，所以∠ACE=90° - 2∠BCD.∠A+∠AEC=90°，∠AEC=70°=∠CED，所以∠CDE=180° - 70° - (90° - 70°)=55°）.
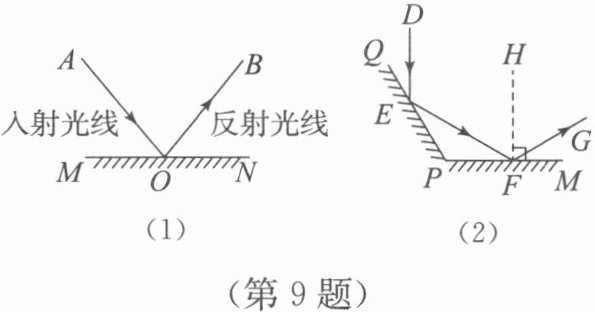
9.（跨学科融合）在学习了平行线和平面镜的相关知识后，同学们进行跨学科综合编题.已知射到平面镜上的光线（入射光线）和变向后的光线（反射光线）与平面镜所夹的角相等.如图（1），MN是平面镜，AO，OB分别为入射光线与反射光线，则∠AOM=∠BON.小明设计如下：如图（2），入射光线DE经镜面PQ与PM反射后，在点F处射出.若HF⊥PM，DE//HF，镜面PQ与PM的夹角即∠QPM=120°，求∠MFG的度数.
答案：60°
因为DE//HF，HF⊥PM，所以DE⊥PM，∠EDP=90°.因为∠QPM=120°，所以∠DQP=180° - 120°=60°.由光的反射定律，∠EDQ=∠FDQ，∠DFP=∠GFP.因为∠EDP=90°，∠DQP=60°，所以∠EDQ=30°，∠FDQ=30°，∠FDP=60°.所以∠DFP=30°，∠GFP=30°，则∠MFG=60°.
