6. 分解因式：
（1）a²b²-ab；
（2）-14abc-7ab+49ab²c．
答案：（1）ab(ab-1)
解析：a²b²-ab=ab·ab-ab·1=ab(ab-1)
（2）-7ab(2c+1-7bc)
解析：-14abc-7ab+49ab²c=-(14abc+7ab-49ab²c)=-7ab·2c+(-7ab)·1+(-7ab)·(-7bc)=-7ab(2c+1-7bc)
7. 现有甲、乙、丙三种卡片各若干张，其中甲、丙两种卡片是正方形，乙种卡片是长方形，卡片的边长如图（1）所示（1＜m＜2）．某同学分别用这些卡片拼出了两个长方形（不重叠无缝隙），如图（2）和图（3），其面积分别为S₁，S₂．
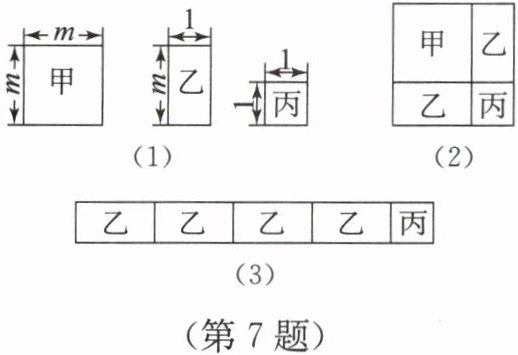
（1）请用含m的代数式分别表示S₁，S₂；
（2）比较S₁与S₂的大小，并说明理由．
答案：（1）S₁=m²+3m+2，S₂=2m²+3m+1
解析：（1）由图（2）可知，长方形的长为(m+1)，宽为(m+2)，所以S₁=(m+1)(m+2)=m²+3m+2；由图（3）可知，长方形的长为(2m+1)，宽为(m+1)，所以S₂=(2m+1)(m+1)=2m²+3m+1
（2）S₂＞S₁
解析：S₂-S₁=(2m²+3m+1)-(m²+3m+2)=m²-1，因为1＜m＜2，所以m²＞1，即m²-1＞0，所以S₂＞S₁
8. 已知a-b=8，ab=6．
（1）求a³b+ab³的值；
（2）求a⁴b²-a³b³+a²b⁴的值．
答案：（1）480
解析：（1）a³b+ab³=ab(a²+b²)=ab[(a-b)²+2ab]，将a-b=8，ab=6代入得6×(8²+2×6)=6×(64+12)=6×76=456
（2）1728
解析：（2）a⁴b²-a³b³+a²b⁴=a²b²(a²-ab+b²)= (ab)²[(a-b)²-ab]，将a-b=8，ab=6代入得6²×(8²-6)=36×(64-6)=36×58=2088
9. （跨学科融合）“回文数”是一种正读倒读皆成句的诗，是我国古典文学作品中一种有趣的特殊体裁．如“遥望四山云接水，碧峰千点数帆轻”，倒过来读，便是“轻帆数点千峰碧，水接云山四望遥”．在数学中有一种正读倒读都一样的自然数，我们称之为“回文数”，例如11，343．
（1）在所有三位数中，“回文数”共有___________个；
（2）任意一个四位数的“回文数”一定是___________的倍数（1除外）．
答案：（1）90
解析：（1）三位数的回文数，百位和个位数字相同，百位数字可以是1-9，有9种选择，十位数字可以是0-9，有10种选择，所以共有9×10=90个
（2）11
解析：（2）设四位数回文数为abba（a、b为数字，a≠0），则这个数为1000a+100b+10b+a=1001a+110b=11×(91a+10b)，所以一定是11的倍数
