知识梳理 三角形的内角和定理：三角形的内角和等于__________. 即在△ABC中，∠A + ∠B + ∠C=______.
答案：180°；180°
【例1】在△ABC中，∠A，∠B，∠C的度数之比为2∶3∶4，则∠B=（ ）.
A. 40°
B. 60°
C. 80°
D. 120°
答案：B
解析：设∠A，∠B，∠C的度数分别为2x，3x，4x. 因为三角形内角和为180°，所以$2x + 3x + 4x = 180°$，$9x = 180°$，$x = 20°$，所以∠B=3x=60°.
跟踪练习1 在△ABC中，如果∠A=$\frac{1}{2}$∠B=$\frac{1}{3}$∠C，求∠A，∠B，∠C的度数.
答案：∠A=30°，∠B=60°，∠C=90°
解析：设∠A=x，则∠B=2x，∠C=3x. 因为∠A + ∠B + ∠C=180°，所以$x + 2x + 3x = 180°$，$6x = 180°$，$x = 30°$，所以∠A=30°，∠B=60°，∠C=90°.
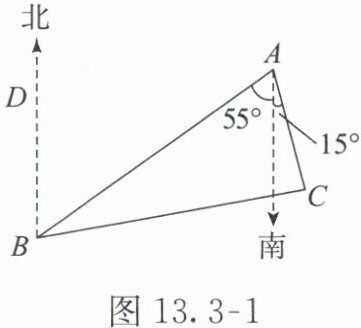
【例2】如图13.3-1，B处在A处的南偏西55°方向，C处在A处的南偏东15°方向，∠DBC=80°，则∠C=（ ）.
（图13.3-1）
A. 75°
B. 85°
C. 95°
D. 100°
答案：B
解析：根据方向角，∠BAC=55° + 15°=70°. 因为AD是正南方向，所以AD//BE（假设BE是正南方向），∠ABD=55°. 因为∠DBC=80°，所以∠ABC=∠DBC - ∠ABD=80° - 55°=25°. 在△ABC中，∠C=180° - ∠BAC - ∠ABC=180° - 70° - 25°=85°.
