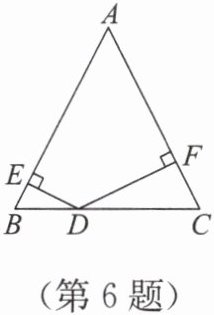
6. 如图,已知△ABC 的面积为 28,AB = AC = 16,D 为边 BC 上一点,过点 D 分别作 DE ⊥ AB,DF ⊥ AC,垂足分别为 E,F. 若 DF = 2DE,则 DF =(
).
A.$\frac{7}{6}$
B.$\frac{16}{3}$
C.$\frac{7}{3}$
D.6
答案:C
解析:
连接AD,设DE=x,则DF=2x。
∵S△ABC=S△ABD+S△ACD,
S△ABD=$\frac{1}{2}$×AB×DE=$\frac{1}{2}$×16×x=8x,
S△ACD=$\frac{1}{2}$×AC×DF=$\frac{1}{2}$×16×2x=16x,
∴8x+16x=28,解得x=$\frac{7}{6}$,
∴DF=2x=2×$\frac{7}{6}$=$\frac{7}{3}$。
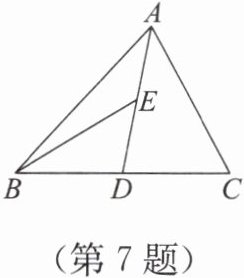
7. 如图,在△ABC 中,D,E 分别是 BC,AD 的中点,$S_{△ABC} = 12 cm²,$则$ S_{△ABE} = $
.
答案:3
解析:
因为D是BC的中点,所以AD是△ABC的中线,根据三角形中线性质,S△ABD = 1/2 S△ABC = 1/2 × 12 = 6 cm²。又因为E是AD的中点,所以BE是△ABD的中线,同理可得S△ABE = 1/2 S△ABD = 1/2 × 6 = 3 cm²。
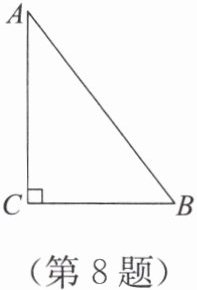
8.(抽象思维)如图,在△ABC 中,∠C = 90°,AC = 8 cm,BC = 6 cm,AB = 10 cm. 若动点 P 从点 C 开始,按 C→A→B→C 的路径运动,速度为 2 cm/s. 设运动的时间为 t s.
(1)当 t 为何值时,CP 把△ABC 的周长分成相等的两部分?
(2)当 t 为何值时,CP 把△ABC 的面积分成相等的两部分?
(3)当 t 为何值时,△BCP 的面积为 12 cm²?
答案:(1)△ABC周长为24cm,一半为12cm。P运动路程为12cm时,t=12÷2=6s。
(2)△ABC面积24cm²,一半12cm²。
①P在AC上:S△BCP=1/2×BC×CP=12,即1/2×6×CP=12,CP=4cm,t=4÷2=2s。
②P在AB中点:AP=5cm,路程CA+AP=13cm,t=13÷2=6.5s。
t=2s或6.5s。
(3)①P在AC上:同(2)①,t=2s。
②P在AB上:S△BCP=12,P为AB中点,t=6.5s。
t=2s或6.5s。