2025年人教金学典同步解析与测评八年级数学上册人教版第13页解析答案

· 跟踪练习2 如图13.3-2，在岸边A点测得湖中小岛P在A点的东北方向(即北偏东$45°$方向)，一轮船从A点出发向正东方向行驶，当轮船行驶到距离小岛P最近时，$∠ APB=$

答案：45°

解析：

过点P作PB⊥AB于点B，此时轮船行驶到B点距离小岛P最近。由题意知∠PAB=45°，在Rt△APB中，∠ABP=90°，所以∠APB=180°-90°-45°=45°。

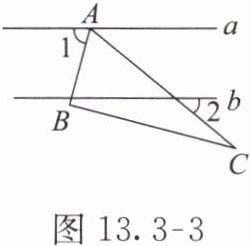
【例3】如图13.3-3，直线$a//b$，点A在直线$a$上. 在$△ ABC$中，$∠ B=90°$，$∠ C=25°$. 若$∠ 1=75°$，则$∠ 2=$(

A.$60°$
B.$40°$
C.$35°$
D.$30°$
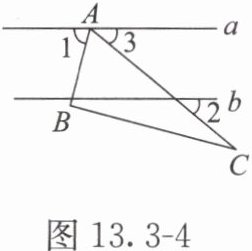
解析如图13.3-4.
因为$∠ B=90°$，$∠ C=25°$，所以$∠ BAC=180°-90°-25°=65°$.
因为$∠ 1=75°$，所以$∠ 3=180°-65°-75°=40°$.
因为直线$a//b$，所以$∠ 2=∠ 3=40°$.

答案 B
总结利用平行线及三角形的内角和定理求度数的关键是要熟练掌握平行线的性质及三角形的内角和等于$180°$.

答案：B

解析：

因为$ ∠ B = 90° $，$ ∠ C = 25° $，
所以$ ∠ BAC = 180° - ∠ B - ∠ C = 180° - 90° - 25° = 65° $。
因为$ ∠ 1 = 75° $，
在$△ ABC$中：
$ ∠ 3 = 180° - ∠ 1 - ∠ BAC = 180° - 75° - 65° = 40° $。
因为直线$ a // b $，
由平行线的性质，内错角相等，得：
$ ∠ 2 = ∠ 3 = 40° $。

· 跟踪练习3 如图13.3-5，$AD//BC$，$BD$平分$∠ ABC$，$∠ A:∠ ABD=3:1$，则$∠ ABD=$

答案：36

解析：

设∠ABD = x，因为BD平分∠ABC，所以∠ABC = 2∠ABD = 2x。
由于AD//BC，根据两直线平行同旁内角互补，得∠A + ∠ABC = 180°。
又∠A:∠ABD = 3:1，故∠A = 3x。
则3x + 2x = 180°，解得x = 36°，即∠ABD = 36°。

1. 如图，在证明$△ ABC$的内角和等于$180°$时，延长$BC$至点$D$，过点$C$作$CE//AB$得到$∠ ECD=∠ ABC$，$∠ BAC=∠ ACE$，由于$∠ BCD=180°$，可得到$∠ ABC+∠ ACB+∠ BAC=180°$，这个证明方法体现的数学思想是(

A.从特殊到一般
B.从一般到特殊
C.数形结合
D.转化

答案：D

解析：

该证明方法通过作辅助线CE//AB，将三角形的三个内角转化为平角∠BCD的三个部分，利用平行线的性质实现了角的转化，从而证明三角形内角和为180°，体现了转化思想。

2. 若一个三角形三个内角的度数之比为$2:4:7$，则这个三角形一定是(

).

A.锐角三角形
B.钝角三角形
C.直角三角形
D.不能确定

答案：B

解析：

设三角形的三个内角的度数分别为$2x$，$4x$，$7x$。
根据三角形内角和定理，得$2x + 4x + 7x = 180°$，
解得$x = \frac{180°}{13}$。
因此，最大角为$7x = 7 × \frac{180°}{13} \approx 96.92° ＞ 90°$，
故该三角形为钝角三角形。