1. 下列计算正确的是（ ）.
A. $a^{3}· a^{4}=a^{12}$
B. $a^{6}÷ a^{2}=a^{3}$
C. $(a^{2})^{3}=a^{6}$
D. $a^{2}-a = a$
答案：C
解析：A选项$a^{3}· a^{4}=a^{3 + 4}=a^{7}$，错误；B选项$a^{6}÷ a^{2}=a^{6 - 2}=a^{4}$，错误；C选项$(a^{2})^{3}=a^{2×3}=a^{6}$，正确；D选项$a^{2}-a$不能合并，错误，故选C.
2. 已知$x^{2}+mxy + 9y^{2}$是完全平方式，则$m = $（ ）.
A. 3
B. -3
C. -6
D. $\pm6$
答案：D
解析：$x^{2}+mxy + 9y^{2}=(x\pm3y)^{2}=x^{2}\pm6xy + 9y^{2}$，所以$m=\pm6$，故选D.
3. 已知$x^{n}=2$，$y^{n}=5$（$n$是正整数），则$(xy)^{3n}=$（ ）.
A. 10
B. 125
C. 133
D. 1000
答案：D
解析：$(xy)^{3n}=(x^{n}y^{n})^{3}=(2×5)^{3}=10^{3}=1000$，故选D.
4. 已知$(x + y)^{2}=49$，$(x - y)^{2}=25$，则$xy=$（ ）.
A. 24
B. 12
C. 6
D. 3
答案：C
解析：$(x + y)^{2}-(x - y)^{2}=4xy = 49 - 25 = 24$，所以$xy = 6$，故选C.
5. 我们知道，$x^{2}=-1$不成立，即不存在平方等于-1的实数. 若我们规定一个新数$i$，使其满足$i^{2}=-1$（即使$x^{2}=-1$成立的条件为$x = i$），并且进一步规定：一切实数可以与新数进行四则运算，且原有的运算法则仍然成立. 于是有$i^{1}=i$，$i^{2}=-1$，$i^{3}=i^{2}· i=(-1)· i=-i$，$i^{4}=(i^{2})^{2}=(-1)^{2}=1$，从而对于任意正整数$n$，可得$i^{4n + 1}=i^{4n}· i=(i^{4})^{n}· i = i$，同理可得$i^{4n + 2}=-1$，$i^{4n + 3}=-i$，$i^{4n}=1$，那么$i + i^{2}+i^{3}+i^{4}+·s+i^{2025}+i^{2026}+i^{2027}$的值为（ ）.
A. 0
B. -1
C. 1
D. i
答案：B
解析：$2027÷4 = 506·s·s3$，原式$=506(i + i^{2}+i^{3}+i^{4})+i^{2025}+i^{2026}+i^{2027}=506×0 + i - 1 - i=-1$，故选B.
6. 化简$3a^{2}(2a - 6)=$ .
答案：$6a^{3}-18a^{2}$
解析：$3a^{2}(2a - 6)=3a^{2}·2a - 3a^{2}·6 = 6a^{3}-18a^{2}$.
7. 计算：$(-\frac{1}{4})^{2025}×4^{2026}=$ .
答案：-4
解析：原式$=(-\frac{1}{4})^{2025}×4^{2025}×4=(-\frac{1}{4}×4)^{2025}×4=(-1)^{2025}×4=-4$.
8. 已知$(y^{2}+my - 3)(2y + n)$的展开式中不含$y$的一次项，常数项是2，则$m$的值为 .
答案：3
解析：展开式为$2y^{3}+(n + 2m)y^{2}+(mn - 6)y - 3n$，常数项$-3n = 2$，得$n=-\frac{2}{3}$，不含一次项则$mn - 6 = 0$，即$m×(-\frac{2}{3})=6$，$m=-9$.
9. 如图（1），从边长为$a$的正方形中剪掉一个边长为$b$的正方形，然后将剩余部分拼成一个如图（2）所示的长方形. 根据图（2）与图（1）的关系写出一个等式： （用含$a$，$b$的代数式表示）.
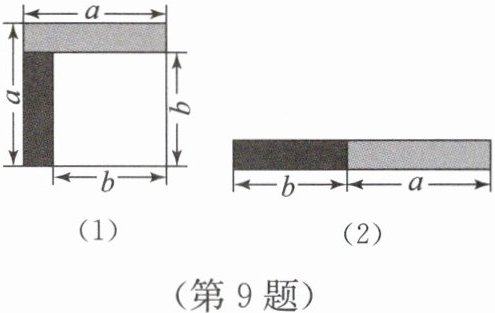
答案：$a^{2}-b^{2}=(a + b)(a - b)$
解析：图（1）面积为$a^{2}-b^{2}$，图（2）长方形长为$a + b$，宽为$a - b$，面积为$(a + b)(a - b)$，故等式为$a^{2}-b^{2}=(a + b)(a - b)$.
10. 计算：
（1）$3xy·2y + x(2x - y^{2})$；
（2）$(2m + n)(m^{2}-n)$.
答案：（1）$2x^{2}+6xy^{2}-xy^{2}$
解析：原式$=6xy^{2}+2x^{2}-xy^{2}=2x^{2}+5xy^{2}$
（2）$2m^{3}-2mn + m^{2}n - n^{2}$
解析：$(2m + n)(m^{2}-n)=2m· m^{2}-2m· n + n· m^{2}-n· n=2m^{3}-2mn + m^{2}n - n^{2}$
