8. （数学思想方法）我国古代数学有许多发现，其中杨辉三角（如图）就是一例.
（第8题）
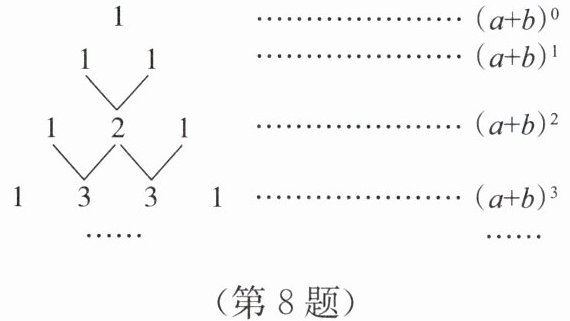
这个三角形的构造法则为两腰上的数都是1，其余每个数均为其上方（左右）两数之和. 事实上，这个三角形给出了$(a + b)^{n}$（$n = 0,1,2,3,·s$）的展开式（按$a$的次数由大到小排列）的系数规律. 例如，在三角形中第三行的三个数1，2，1恰好对应着$(a + b)^{2}$的展开式$a^{2}+2ab + b^{2}$中各项的系数；第四行的四个数1，3，3，1恰好对应着$(a + b)^{3}$的展开式$a^{3}+3a^{2}b + 3ab^{2}+b^{3}$中各项的系数；等等.
（1）根据上面的规律，$(a + b)^{4}$的展开式的各项系数中最大的为 ；
（2）求$2^{5}+5×2^{4}×(-3)+10×2^{3}×(-3)^{2}+10×2^{2}×(-3)^{3}+5×2×(-3)^{4}+(-3)^{5}$的值；
（3）若$(2x - 1)^{2025}=a_{1}x^{2025}+a_{2}x^{2024}+a_{3}x^{2023}+·s+a_{2024}x^{2}+a_{2025}x + a_{2026}$，求$a_{1}+a_{2}+a_{3}+·s+a_{2023}+a_{2024}+a_{2025}$的值.
答案：（1）6
解析：$(a + b)^{4}$的展开式系数为1，4，6，4，1，最大的是6
（2）-1
解析：原式$=[2 + (-3)]^{5}=(-1)^{5}=-1$
（3）$2^{2025}-1$
解析：令$x = 1$，得$(2×1 - 1)^{2025}=a_{1}+a_{2}+·s+a_{2025}+a_{2026}$，即$1 = a_{1}+a_{2}+·s+a_{2026}$，又令$x = 0$，得$a_{2026}=(-1)^{2025}=-1$，所以$a_{1}+·s+a_{2025}=1 - a_{2026}=1 - (-1)=2$.
