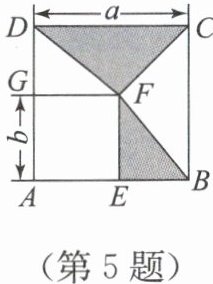
5. 两个正方形$ABCD$,$AEFG$如图摆放,边长分别为$a$,$b$。若$a^{2}+b^{2}=34$,$BE = 2$,求图中阴影部分的面积。
答案:8
解析:
∵四边形ABCD和AEFG是正方形,边长分别为a,b,
∴AB=BC=CD=AD=a,AE=EF=FG=AG=b,∠A=∠B=∠C=∠D=∠E=∠F=∠G=90°。
由题意,BE=2,且E在AB上,∴AB - AE = BE,即a - b = 2。
阴影部分面积为△DFC与△BEF的面积之和。
在△BEF中,BE = a - b = 2,EF = b,∠BEF=90°,
∴S△BEF = $\frac{1}{2}×BE×EF$ = $\frac{1}{2}×2×b$ = b。
在△DFC中,DC = a,DC边上的高为a - b = 2,
∴S△DFC = $\frac{1}{2}×DC×高$ = $\frac{1}{2}×a×2$ = a。
∴阴影部分面积S = S△BEF + S△DFC = a + b。
已知a² + b² = 34,a - b = 2,
∵(a - b)² = a² - 2ab + b²,∴2² = 34 - 2ab,解得ab = 15。
∵(a + b)² = a² + 2ab + b² = 34 + 2×15 = 64,∴a + b = 8(a,b>0)。
故阴影部分面积为8。
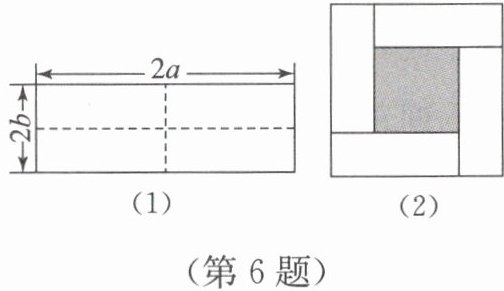
6. 在一次数学活动中,小红将一个长为$2a$、宽为$2b$的长方形沿如图(1)所示的虚线用剪刀均分成四个全等的小长方形,然后按图(2)的方式拼成一个正方形。小红通过观察图(1)(2),用两种不同的方法表示出了图(2)中阴影部分的面积,并得出$(a + b)^{2}$,$(a - b)^{2}$,$ab$这三个代数式之间的一个等量关系。
(1)请写出代数式$(a + b)^{2}$,$(a - b)^{2}$,$ab$的一个等量关系,并说明理由;
(2)根据(1)中的等量关系,解决如下问题:若$x + y = 6$,$xy = 4$,求$(x - y)^{2}$的值。
答案:(1)
关系:$(a - b)^{2}=(a + b)^{2}-4ab$。
理由:
图(2)中正方形的边长为$a + b$,其面积$S=(a + b)^{2}$。
阴影部分是小正方形,边长为$a - b$,面积$S_{阴}=(a - b)^{2}$。
四个小长方形面积和为$4ab$,且大正方形面积等于四个小长方形面积与阴影部分面积之和,即$(a + b)^{2}=(a - b)^{2}+4ab$,移项可得$(a - b)^{2}=(a + b)^{2}-4ab$。
(2)
由(1)知$(x - y)^{2}=(x + y)^{2}-4xy$,
把$x + y = 6$,$xy = 4$代入上式得:
$(x - y)^{2}=6^{2}-4×4=36 - 16=20$。
7. 【教材再现】人教版义务教育教科书数学八年级上册习题16.3(拓广探索)第7题:
已知$a + b = 5$,$ab = 3$,求$a^{2}+b^{2}$的值。
【习题讲解】老师讲解了解答这道题的两种方法:
|方法一|方法二|
|----|----|
|因为$a + b = 5$,
所以$(a + b)^{2}=25$。
所以$a^{2}+2ab + b^{2}=25$。
又因为$ab = 3$,
所以$a^{2}+b^{2}=25 - 2ab = 25 - 6 = 19$。|因为$(a + b)^{2}=a^{2}+2ab + b^{2}$,
所以$a^{2}+b^{2}=(a + b)^{2}-2ab$。
又因为$a + b = 5$,$ab = 3$,
所以$a^{2}+b^{2}=25 - 6 = 19$。|
【方法运用】请你参照上面两种方法,解答以下问题:
(1)已知$a - b = 2$,$a^{2}+b^{2}=12$,求$ab$的值;
(2)已知$a+\dfrac{1}{a}=4$,求$(a-\dfrac{1}{a})^{2}$的值。
答案:(1)
方法一:
因为$a - b = 2$,所以$(a - b)^{2}=4$,即$a^{2}-2ab + b^{2}=4$。
又因为$a^{2}+b^{2}=12$,所以$12 - 2ab = 4$,解得$ab = 4$。
方法二:
因为$(a - b)^{2}=a^{2}-2ab + b^{2}$,所以$a^{2}+b^{2}=(a - b)^{2}+2ab$,则$ab=\frac{(a^{2}+b^{2})-(a - b)^{2}}{2}$。
把$a - b = 2$,$a^{2}+b^{2}=12$代入可得$ab=\frac{12 - 4}{2}=4$。
(2)
因为$(a+\frac{1}{a})^{2}=a^{2}+2+\frac{1}{a^{2}} = 16$,所以$a^{2}+\frac{1}{a^{2}}=16 - 2 = 14$。
又因为$(a-\frac{1}{a})^{2}=a^{2}-2+\frac{1}{a^{2}}$,把$a^{2}+\frac{1}{a^{2}}=14$代入可得$(a-\frac{1}{a})^{2}=14 - 2 = 12$。