跟踪练习1 运用完全平方公式计算:
(1)$53^{2}$; (2)$97^{2}$;
(3)$700.1^{2}$; (4)$499.9^{2}$。
答案:(1)
$53^{2}$
$=(50 + 3)^{2}$
$=50^{2} + 2 × 50 × 3 + 3^{2}$
$=2500 + 300 + 9$
$=2809$
(2)
$97^{2}$
$=(100 - 3)^{2}$
$=100^{2} - 2 × 100 × 3 + 3^{2}$
$=10000 - 600 + 9$
$=9409$
(3)
$700.1^{2}$
$=(700 + 0.1)^{2}$
$=700^{2} + 2 × 700 × 0.1 + 0.1^{2}$
$=490000 + 140 + 0.01$
$=490140.01$
(4)
$499.9^{2}$
$=(500 - 0.1)^{2}$
$=500^{2} - 2 × 500 × 0.1 + 0.1^{2}$
$=250000 - 100 + 0.01$
$=249900.01$
【例2】已知$a^{2}+b^{2}=26$,$ab = 3$,求$(a + b)^{2}$和$(a - b)^{2}$的值。
解 $(a + b)^{2}=a^{2}+b^{2}+2ab = 26 + 2× 3 = 32$,$(a - b)^{2}=a^{2}+b^{2}-2ab = 26 - 2× 3 = 20$。
总结 利用完全平方公式求代数式的值时,一定要熟悉完全平方公式的变形。
完全平方公式的常见变形有
$a^{2}+b^{2}=(a + b)^{2}-2ab=(a - b)^{2}+2ab$;
$(a + b)^{2}=(a - b)^{2}+4ab$。
答案:答题卡答:
$(a + b)^{2}=a^{2} + 2ab + b^{2}$
$=a^{2}+b^{2}+2ab$
因为$a^{2}+b^{2}=26$,$ab = 3$,
则$2ab=2×3 = 6$,
所以$a^{2}+b^{2}+2ab=26 + 6=32$。
$(a - b)^{2}=a^{2}-2ab + b^{2}$
$=a^{2}+b^{2}-2ab$
因为$a^{2}+b^{2}=26$,$2ab = 6$,
所以$a^{2}+b^{2}-2ab=26-6 = 20$。
综上$(a + b)^{2}$的值为$32$,$(a - b)^{2}$的值为$20$。
跟踪练习2 已知$(a + b)^{2}=12$,$ab = 2$,则$(a - b)^{2}$的值为(
)。
A.$4$
B.$8$
C.$16$
D.$20$
答案:A
解析:
根据完全平方公式,$(a+b)^2 = a^2 + 2ab + b^2$,$(a-b)^2 = a^2 - 2ab + b^2$。
已知$(a+b)^2=12$,$ab=2$,则:
$(a-b)^2$
$=a^2 - 2ab + b^2$
$=a^2 + 2ab + b^2 - 4ab$
$=(a+b)^2 - 4ab$
将已知数值代入:
$(a-b)^2$
$=12 - 4 × 2$
$=12 - 8$
$=4$
1. 小华在利用完全平方公式计算一个二项式的平方时,不小心用墨水把中间一项的系数染黑了,他得到的正确结果为$a^{2}$■$ab + 9b^{2}$,则中间一项的系数是(
)。
A.$-6$
B.$6$
C.$6$或$-6$
D.$18$
答案:C
解析:
因为完全平方公式为$(m \pm n)^2 = m^2 \pm 2mn + n^2$,已知结果为$a^{2}$■$ab + 9b^{2}$,其中$a^2=(a)^2$,$9b^2=(3b)^2$,所以中间项应为$\pm 2 × a × 3b = \pm 6ab$,故中间一项的系数是$6$或$-6$。
2. 下列等式不成立的是(
)。
A.$(a + b)^{2}=(-a - b)^{2}$
B.$(a - b)^{2}=a^{2}-b^{2}$
C.$(a - b)^{2}=(b - a)^{2}$
D.$(-a + b)^{2}=(-b + a)^{2}$
答案:B
解析:
选项A,对于$(a + b)^{2}$和$(-a - b)^{2}$,因为$(-a - b)^{2}=[-(a+b)]^{2}=(a+b)^2$,所以该等式成立。
选项B,根据完全平方公式,$(a - b)^{2}=a^{2}-2ab+b^{2}$,而$a^{2}-b^{2}=(a + b)(a - b)$,所以$(a - b)^{2}≠ a^{2}-b^{2}$,该等式不成立。
选项C,对于$(a - b)^{2}$和$(b - a)^{2}$,因为$(b - a)^{2}=[-(a - b)]^{2}=(a - b)^{2}$,所以该等式成立。
选项D,对于$(-a + b)^{2}$和$(-b + a)^{2}$,因为$(-a + b)^{2}=(b - a)^{2}$,$(-b + a)^{2}=(a - b)^{2}=(b - a)^{2}$,所以该等式成立。
3. 若$a^{2}+b^{2}=16$,$ab = 6$,则$a - b$的值为(
)。
A.$-2$
B.$2$
C.$\pm 2$
D.$\pm 3$
答案:C
解析:
根据完全平方公式,$(a - b)^{2} = a^{2} - 2ab + b^{2}$,
已知$a^{2} + b^{2} = 16$,$ab = 6$,将其代入公式可得:
$(a - b)^{2}=a^{2}+b^{2}-2ab = 16 - 2×6 = 16 - 12 = 4$。
因为一个数的平方等于$4$,那么这个数为$\pm\sqrt{4}=\pm2$,所以$a - b = \pm 2$。
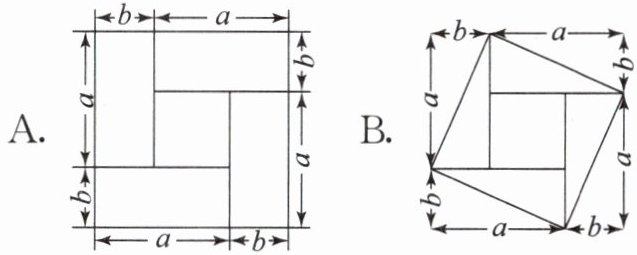
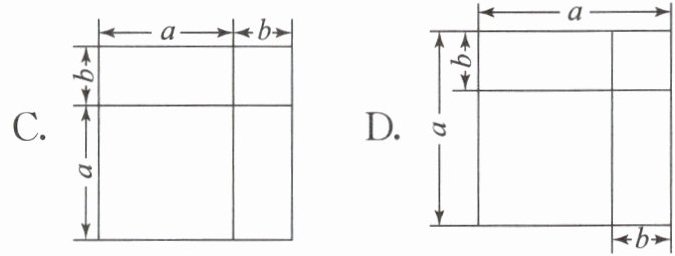
4. 在下列正方形分割方案中,可以验证$(a + b)^{2}=(a - b)^{2}+4ab$的图形是(
)。
A.
B.
C.
D.
答案:A
解析:
要验证$(a + b)^2=(a - b)^2 + 4ab$,需大正方形(边长$a + b$)面积等于小正方形(边长$a - b$)面积与4个面积为$ab$的图形面积之和。选项A中,大正方形边长为$a + b$,可分割为中心边长$a - b$的小正方形和四周4个面积为$ab$的长方形,总面积为$(a - b)^2 + 4ab$,等于大正方形面积$(a + b)^2$,符合公式。