4. 如图(1),将边长为 $a$ 的大正方形纸片剪去一个边长为 1 的小正方形(阴影部分),并将剩余部分沿虚线剪开,得到两个长方形,再将这两个长方形拼成如图(2)所示的长方形,这两个图能解释的一个等式是
.
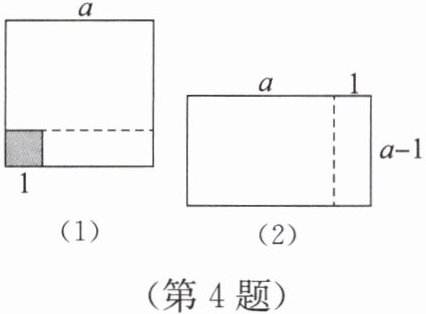
答案:$a^2 - 1 = (a + 1)(a - 1)$
解析:
图(1)剩余部分面积为大正方形面积减去小正方形面积,即$a^2 - 1^2$。图(2)长方形的长为$a + 1$,宽为$a - 1$,面积为$(a + 1)(a - 1)$。因为两图剩余部分面积相等,所以$a^2 - 1 = (a + 1)(a - 1)$。
5. 运用平方差公式计算:
(1) $103×97$;
(2) $(a+2)(a-2)(a^2+4)$。
答案:(1)
$\begin{aligned}&103 × 97 \\=&(1 0 0 + 3)(1 0 0 - 3) \\=&1 0 0 ^ { 2 } - 3 ^ { 2 } \\=&1 0 0 0 0 - 9 \\=&9 9 9 1 \\\end{aligned}$
(2)
$\begin{aligned}&(a + 2)(a - 2)(a ^ { 2 } + 4) \\=&(a ^ { 2 } - 2 ^ { 2 })(a ^ { 2 } + 4) \\=&(a ^ { 2 } - 4)(a ^ { 2 } + 4) \\=&(a ^ { 2 } ) ^ { 2 } - 4 ^ { 2 } \\=&a ^ { 4 } - 1 6 \\\end{aligned}$
6. (1) 数学课堂上,老师出了一道数学题,如图(1),用代数式表示绿地(空白部分)的面积。甲、乙两名同学的答案分别是 $12×8-12x-8x$,$(12-x)(8-x)$,则答案正确的同学是
.
(2) 如图(2),有一块长为 $(8a+3b)$ m、宽为 $(7a-3b)$ m 的长方形空地,计划修筑东西、南北走向的两条道路,其余进行绿化。已知两条道路的宽分别为 $2a$ m 和 $3a$ m,求绿化的面积(用含 $a$,$b$ 的代数式来表示)。
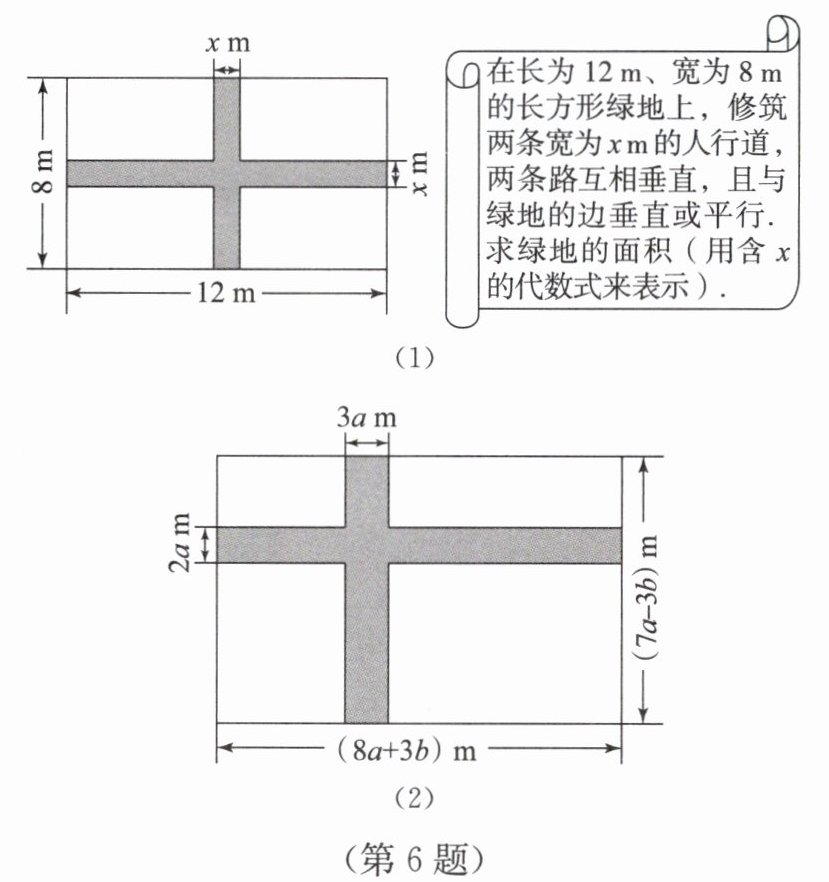
答案:(1) 乙
(2) 绿化面积为:
$\begin{aligned}&(8a + 3b - 3a)(7a - 3b - 2a)\\=&(5a + 3b)(5a - 3b)\\=&(5a)^2 - (3b)^2\\=&25a^2 - 9b^2\end{aligned}$
答:绿化面积为$25a^2 - 9b^2$平方米。
7. (新定义)一个非零自然数若能表示为两个非零自然数的平方差,则称这个自然数为“智慧数”。比如 $28=8^2-6^2$,故 28 是一个“智慧数”。下列各数中,不是“智慧数”的是(
)。
A.30
B.32
C.987
D.988
答案:A
解析:
智慧数可表示为$a^2 - b^2=(a - b)(a + b)$,其中$a,b$为非零自然数,$a > b$,且$(a - b)$与$(a + b)$同奇或同偶。
A.30:因数对(1,30),(2,15),(3,10),(5,6)均奇偶不同,无法分解为同奇或同偶因数乘积,不是智慧数。
B.32:$32=2×16$(同偶),$a=(2+16)/2=9$,$b=(16-2)/2=7$,$32=9^2 - 7^2$,是智慧数。
C.987:$987=1×987$(同奇),$a=(1+987)/2=494$,$b=(987-1)/2=493$,$987=494^2 - 493^2$,是智慧数。
D.988:$988=26×38$(同偶),$a=(26+38)/2=32$,$b=(38-26)/2=6$,$988=32^2 - 6^2$,是智慧数。