【例1】下列多项式的乘法中,可以用平方差公式计算的是(
)。
A.$(y+1)(-y-1)$
B.$(2+x^2)(2-x^2)$
C.$(-x+y)(x-y)$
D.$(x^2+y)(x-y^2)$
答案 B
总结 用平方差公式计算的关键是把握平方差公式的典型特征:既有“相同项”,又有“相反项”,而结果是“相同项”的平方减去“相反项”的平方,千万不要颠倒了。
答案:B
解析:
平方差公式为$a^2 - b^2 = (a + b)(a - b)$,其特征为两个二项式相乘,其中一项完全相同,另一项互为相反数。
选项A:$(y + 1)(-y - 1)=-(y + 1)(y + 1)=-(y + 1)^2$,两项都互为相反数,不能用平方差公式计算。
选项B:$(2 + x^2)(2 - x^2)=2^2-(x^2)^2$,符合平方差公式特征,可以用平方差公式计算。
选项C:$(-x + y)(x - y)=-(x - y)(x - y)=-(x - y)^2$,两项都互为相反数,不能用平方差公式计算。
选项D:$(x^2 + y)(x - y^2)$,相同项和相反项不明显,不能用平方差公式计算。
· 跟踪练习1 运用平方差公式计算:
(1) $(2x+3y)(2x-3y)$;
(2) $(x^3+3)(x^3-3)$;
(3) $(-2m+n)(-2m-n)$。
答案:(1) $(2x+3y)(2x-3y)=(2x)^2-(3y)^2=4x^2-9y^2$;
(2) $(x^3+3)(x^3-3)=(x^3)^2-3^2=x^6-9$;
(3) $(-2m+n)(-2m-n)=(-2m)^2-n^2=4m^2-n^2$。
【例2】如果 $x^2-y^2=12$,$x+y=4$,则 $x-y=$
.
解析 因为 $x^2-y^2=12$,
所以 $(x+y)(x-y)=12$.
又因为 $x+y=4$,
所以 $x-y=3$.
答案 3
总结 解决此题的关键是利用平方差公式进行恒等变形,然后整体代入进行求值。
答案:3
解析:
因为$x^{2}-y^{2}=12$,根据平方差公式$a^2 - b^2=(a + b)(a - b)$,这里$a = x$,$b = y$,所以$(x + y)(x - y)=12$。
又因为$x + y = 4$,将其代入$(x + y)(x - y)=12$中,可得$4(x - y)=12$,则$x - y = 3$。
· 跟踪练习2 已知 $m+n=3$,$m-n=4$,则 $m^2-n^2$ 的值为(
)。
A.$-12$
B.12
C.$-25$
D.25
答案:B
解析:
根据平方差公式,$m^2 - n^2 = (m + n)(m - n)$,将已知条件$m + n = 3$,$m - n = 4$代入可得:$m^2 - n^2 = 3 × 4 = 12$。
1. 下列计算正确的是(
)。
A.$(2x-y)(x+2y)=2x^2-2y^2$
B.$(-x+y)(x-y)=x^2-y^2$
C.$(-x-2y)(-x+2y)=x^2-4y^2$
D.$(x+2y)(x-2y)=x^2-2y^2$
答案:C
解析:
选项A:$(2x-y)(x+2y)=2x^2 + 4xy - xy - 2y^2 = 2x^2 + 3xy - 2y^2$,故A错误;
选项B:$(-x + y)(x - y) = -(x - y)(x - y) = -(x - y)^2 = -x^2 + 2xy - y^2$,故B错误;
选项C:$(-x - 2y)(-x + 2y) = (-x)^2 - (2y)^2 = x^2 - 4y^2$,故C正确;
选项D:$(x + 2y)(x - 2y) = x^2 - (2y)^2 = x^2 - 4y^2$,故D错误。
2. 若 $a+b=3$,则 $a^2-b^2+3b-3a$ 的值为(
)。
A.0
B.3
C.6
D.9
答案:A
解析:
$\begin{aligned}a^2 - b^2 + 3b - 3a &= (a^2 - b^2) - 3(a - b) \\&= (a + b)(a - b) - 3(a - b) \\&= (a - b)(a + b - 3)\end{aligned}$
因为 $a + b = 3$,所以 $a + b - 3 = 0$,则原式 $= (a - b) × 0 = 0$。
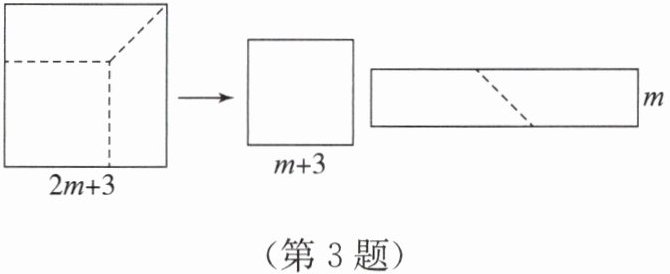
3. 如图,将边长为 $2m+3$ 的正方形纸片剪出一个边长为 $m+3$ 的正方形之后,剩余部分可剪拼成一个长方形。拼成的长方形的面积是(
)。
A.$3m+6$
B.$3m^2+6m$
C.$4m^2+12m+9$
D.$2m^2+6m+9$
答案:M(原题选项对应为M(即B)选项,即输出):B
解析:
设原正方形的边长为$2m+3$,则其面积为$(2m+3)^2$。剪出一个边长为$m+3$的正方形,其面积为$(m+3)^2$。
剩余部分的面积为:
$(2m+3)^2 - (m+3)^2$
$=(4m^2 + 12m + 9) - (m^2 + 6m + 9)$
$= 4m^2 + 12m + 9 - m^2 - 6m - 9$
$= 3m^2 + 6m$
所以拼成的长方形的面积为$3m^2 + 6m$。