2025年人教金学典同步解析与测评八年级数学上册人教版第100页解析答案

●跟踪练习1 已知(x−3)(x+8)=
x²十mx十n，那么m，n的值分别是(

).
A.24,−5 B.5,−24
C.−24,5 D.−5,−24

答案：B

解析：

将 $(x - 3)(x + 8)$ 展开，使用分配律进行整式的乘法运算：
$(x - 3)(x + 8) = x · x + x · 8 - 3 · x - 3 × 8$
$= x^2 + 8x - 3x - 24$
$= x^2 + 5x - 24$
与 $x^2 + mx + n$ 进行对比，可以得到：
$m = 5$，
$n = -24$，
综上所述，本题答案是：B。

[例2]设有边长分别为a和b(a＞b)
的A类和B类正方形纸片以及长为a且宽为
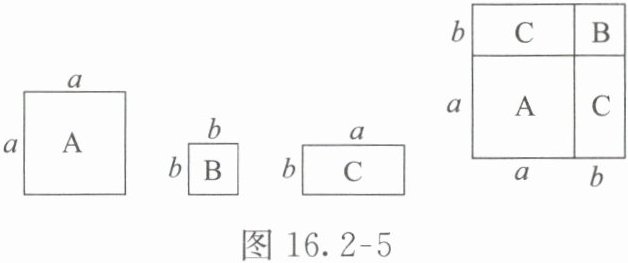
b的C类长方形纸片若干张.如图16.2−5，
要拼一个边长为a十b的正方形，需要1张A 类纸片、1张B类纸片和2张C类纸片.若要拼一个长为3a十b、宽为2a+2b的长方形，则需要C类纸片的张数为(

A.6
B.7
C.8
D.9
解析因为长为3a十b、宽为2a+2b的
长方形的面积为(3a+b)(2a+2b)=6a²十
6ab+2ab+2b²=6a²+2b²+8ab,
所以需要6张A类纸片、2张B类纸片
和8张C类纸片.
答案 C
总结解题时先理解题意，将题中涉及
的未知量用代数式表示出来，然后利用多项
式与多项式相乘的法则进行运算，最后通过
合并同类项将结果化为最简形式.

答案：C

解析：

要拼一个长为 $3a + b$，宽为 $2a + 2b$ 的长方形，其面积为：
$(3a + b)(2a + 2b)$
展开得：
$3a × 2a + 3a × 2b + b × 2a + b × 2b$
$= 6a^{2} + 6ab + 2ab + 2b^{2}$
$= 6a^{2} + 8ab + 2b^{2}$
根据各类纸片的面积：
A类纸片面积为 $a^{2}$，需要6张；
B类纸片面积为 $b^{2}$，需要2张；
C类纸片面积为 $ab$，需要8张。
所以需要C类纸片的张数为8。

.跟踪练习2 某校要举行校庆活动，
现计划在教学楼之间的广场上搭建舞台.已
知广场中心有一座边长为b的正方形花坛.
有以下两种方案:
方案一，如图16.2−6(1)，围绕花坛搭
建外围为正方形的“回”字形舞台(阴影部
分)，舞台的面积记为S1;
方案二，如图16.2−6(2)，在花坛的三
面搭建“凹”字形舞台(阴影部分)，舞台的
面积记为S2.

则下列说法一定正确的是(

).

A.S=(a−b)²
B.S2=a²−b²
C.S1−S2=b2
D.S1.S2=a4+b4

答案：C

解析：

方案一：“回”字形舞台面积$S_1$为外围正方形面积减去花坛面积，外围正方形边长为$a$，花坛边长为$b$，则$S_1 = a^2 - b^2$。
方案二：“凹”字形舞台面积$S_2$，由图(2)可知，外围总尺寸为边长$a$的正方形，空白部分为花坛（面积$b^2$）和凹进去的边长为$b$的正方形（面积$b^2$），故$S_2 = a^2 - 2b^2$。
则$S_1 - S_2 = (a^2 - b^2) - (a^2 - 2b^2) = b^2$。

1.下列各式中，计算结果是x²+7x一
18的是(

).

A.(x+2)(x+9)
B.(x−1)(x+18)
C.(x−2)(x+9)
D.(x−3)(x+6)

答案：C

解析：

根据多项式乘法法则，分别计算各选项的结果：
A. $(x+2)(x+9) = x^2 + 9x + 2x + 18 = x^2 + 11x + 18$
B. $(x-1)(x+18) = x^2 + 18x - x - 18 = x^2 + 17x - 18$
C. $(x-2)(x+9) = x^2 + 9x - 2x - 18 = x^2 + 7x - 18$
D. $(x-3)(x+6) = x^2 + 6x - 3x - 18 = x^2 + 3x - 18$
通过对比，选项C的计算结果为$x^2 + 7x - 18$。

2.计算(m²+1)(m+2)的结果中,
m²项的系数是(

).

A.3
B.2
C.1
D.0

答案：B

解析：

根据多项式乘法法则，将$(m^2 + 1)$中的每一项与$(m + 2)$中的每一项相乘，得：
$(m^2 + 1)(m + 2)$
$=m^2× m+m^2×2 + 1× m + 1×2$
$=m^3 + 2m^2 + m + 2$
所以在$m^2$项的系数是$2$。