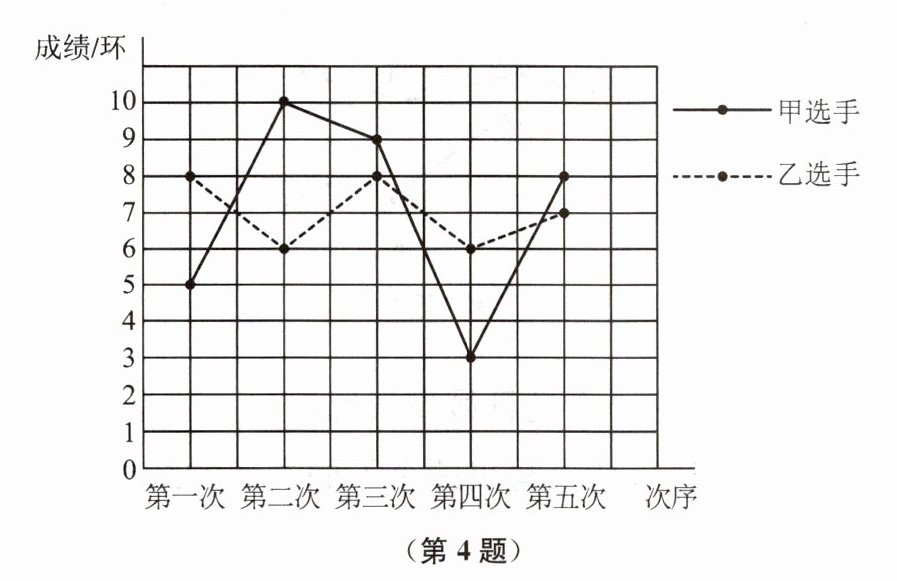
4. 某射击运动队进行了五次射击测试,甲、乙两名选手的测试成绩如图所示,甲、乙两名选手成绩的方差分别记为$s_{甲}^{2}$、$s_{乙}^{2}$,则$s_{甲}^{2}$
>
(填“>”“<”或“=”)$s_{乙}^{2}$.
解析:
由图可知,甲选手五次成绩为:5,10,9,3,8;乙选手五次成绩为:8,6,8,6,7。
甲的平均成绩:$\overline{x}_{甲}=\frac{5 + 10 + 9 + 3 + 8}{5} = 7$
甲的方差:$s_{甲}^{2}=\frac{1}{5}[(5 - 7)^{2}+(10 - 7)^{2}+(9 - 7)^{2}+(3 - 7)^{2}+(8 - 7)^{2}]$
$=\frac{1}{5}[(-2)^{2}+3^{2}+2^{2}+(-4)^{2}+1^{2}]$
$=\frac{1}{5}(4 + 9 + 4 + 16 + 1)=\frac{34}{5}=6.8$
乙的平均成绩:$\overline{x}_{乙}=\frac{8 + 6 + 8 + 6 + 7}{5}=7$
乙的方差:$s_{乙}^{2}=\frac{1}{5}[(8 - 7)^{2}+(6 - 7)^{2}+(8 - 7)^{2}+(6 - 7)^{2}+(7 - 7)^{2}]$
$=\frac{1}{5}[1^{2}+(-1)^{2}+1^{2}+(-1)^{2}+0^{2}]$
$=\frac{1}{5}(1 + 1 + 1 + 1 + 0)=\frac{4}{5}=0.8$
因为$6.8>0.8$,所以$s_{甲}^{2}>s_{乙}^{2}$
>